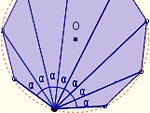
 Rozważamy średnią długości przekątnych n-kąta foremnego wpisanego w okrąg o promieniu R. Uzasadnimy (prawie elementarnie), że dla dla dużych n jest ona niemal równa 4/
Rozważamy średnią długości przekątnych n-kąta foremnego wpisanego w okrąg o promieniu R. Uzasadnimy (prawie elementarnie), że dla dla dużych n jest ona niemal równa 4/Odlotowe figury
Średnia długości przekątnych
 Rozważamy średnią długości przekątnych n-kąta foremnego wpisanego w okrąg o promieniu R. Uzasadnimy (prawie elementarnie), że dla dla dużych n jest ona niemal równa 4/
Rozważamy średnią długości przekątnych n-kąta foremnego wpisanego w okrąg o promieniu R. Uzasadnimy (prawie elementarnie), że dla dla dużych n jest ona niemal równa 4/
Średnia długości przekątnych (tylko dla dorosłych)
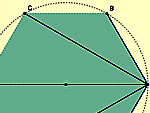 Wyznaczymy średnie długości przekątnych n-kątów foremnych
wpisanych w okrąg o promieniu R. Dla dużych wartości n są one niemal równe 4 /
Wyznaczymy średnie długości przekątnych n-kątów foremnych
wpisanych w okrąg o promieniu R. Dla dużych wartości n są one niemal równe 4 /
![]() . R. Jest to uzupełnienie artykułu Średnia długości przekątnych, w którym to samo robimy poglądowo i niemal elementarnie.
. R. Jest to uzupełnienie artykułu Średnia długości przekątnych, w którym to samo robimy poglądowo i niemal elementarnie.
Trójkąty Reuleaux 3D
 Kula 'ciasno zapakowana' pomiędzy dwie równoległe płaszczyzny 'rozpycha' je zawsze na ten sam dystans, niezależnie od położenia w przestrzeni tych równoległych płaszczyzn. Nie tylko kula ma taką własność. Zanim zobaczysz, jak wyglądają inne takie bryły, zajrzyj do tekstu Trójkąty Reuleaux mówiącego o podobnym zjawisku na płaszczyźnie.
Kula 'ciasno zapakowana' pomiędzy dwie równoległe płaszczyzny 'rozpycha' je zawsze na ten sam dystans, niezależnie od położenia w przestrzeni tych równoległych płaszczyzn. Nie tylko kula ma taką własność. Zanim zobaczysz, jak wyglądają inne takie bryły, zajrzyj do tekstu Trójkąty Reuleaux mówiącego o podobnym zjawisku na płaszczyźnie.
Środki figur płaskich
 Zamieszczony tu tekst wymaga zastanowienia, samodzielnej pracy, tworzenia własnych rysunków.
Warto wcześniej zrobić kilka zadań z artykułów:
Środki par zbiorów,
Środki zbiorów liczb.
Zobaczysz tu dowody twierdzeń o tym, że środki pewnych figur są generowane przez brzegi tych figur.
Zamieszczony tu tekst wymaga zastanowienia, samodzielnej pracy, tworzenia własnych rysunków.
Warto wcześniej zrobić kilka zadań z artykułów:
Środki par zbiorów,
Środki zbiorów liczb.
Zobaczysz tu dowody twierdzeń o tym, że środki pewnych figur są generowane przez brzegi tych figur.
Odcinek figur
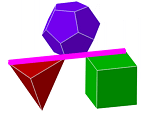 W artykule Środki par zbiorów można zobaczyć, jak tworzyć zbiór środkowy dla danych dwóch figur A i B, czyli zbiór środków odcinków łączących te figury. Leży on pomiędzy A i B. Tym razem utworzymy całą kolekcję zbiorów płynnie przechodzących od figury A do figury B, czyli odcinek figur. Jak to wygląda? Zobacz.
W artykule Środki par zbiorów można zobaczyć, jak tworzyć zbiór środkowy dla danych dwóch figur A i B, czyli zbiór środków odcinków łączących te figury. Leży on pomiędzy A i B. Tym razem utworzymy całą kolekcję zbiorów płynnie przechodzących od figury A do figury B, czyli odcinek figur. Jak to wygląda? Zobacz.







