Zawracanie trójkąta

Wprowadzasz rower do komórki - to łatwe. Gorzej jest z wyprowadzaniem, wygodniej by było najpierw go odwrócić. Komórka jest jednak dość ciasna. Czy można w niej zawrócić rower?
Rozważamy tu tylko najprostsze komórki - trójkąty ABC i najprostsze rowery - odcinki i trójkąty równoboczne. Wiele faktów podajemy bez uzasadnień, bo niektóre są dość trudne.

Niech figura F będzie zawarta w figurze G. Będziemy mówili, że F jest obracalna w G, jeśli istnieje taki ruch (niekoniecznie obrót) figury F w obrębie G, że w trakcie tego ruchu F okręca się o pełne 360^o.

Gdy figura F, zawarta w trójkącie ABC, leży w kole wpisanym w ten trójkąt, to F jest obracalna w obrębie ABC. Wystarczy po prostu obracać ją względem środka koła.

 
Odcinek F będący wysokością trójkąta równobocznego ABC, jest obracalny w obrębie ABC. Pokazany na rysunku ruch odcinka jest kombinacją obrotów i przesunięć.
Odcinki zawarte w trójkącie równobocznym równoległe do wysokości są od niej krótsze, zatem żaden odcinek dłuższy od wysokości nie jest obracalny w tym trójkącie.

Podobnie można uzasadnić nieco ogólniejsze twierdzenie.

Twierdzenie 1.  
Odcinek F zawarty w trójkącie ABC jest obracalny w ABC wtedy i tylko wtedy, gdy F jest nie dłuższy od najkrótszej wysokości trójkąta ABC.

Dalej zajmować się będziemy obracalnością trójkątów równobocznych w obrębie trójkąta ABC.

Dowód.   Obracalny trójkąt równoboczny P'Q'R' można tak przemieścić w obrębie trójkąta ABC, że uzyskany trójkąt P''Q''R'' ma boki równoległe do trójkąta PQR. Gdyby był większy, to bok P''Q'' musiałby leżeć pomiędzy PQ i R (bo gdzie indziej jest za mało miejsca). Jednak wtedy wierzchołek R'' wystawałby poza trójkąt ABC.

Twierdzenie 3.  
Niech przystające trójkąty równoboczne PQR, P'Q'R' będą zawarte w trójkącie ABC.
Jeśli P'Q'R' jest obracalny w ABC, to PQR jest też obracalny w ABC.

Dowód.   W trakcie ruchu P'Q'R' w obrębie ABC jest takie położenie P''Q''R'', w którym boki trójkąta P''Q''R'' są równoległe do boków trójkąta PQR. Zatem istnieje przesunięcie, które nałoży PQR na P''Q''R''. W trakcie przesuwania PQR stale będzie on w obrębie trójkąta ABC (wypukłość), zatem trójkąt PQR jest obracalny, bo możliwy jest następujący ruch: przesuwamy go do P''Q''R'', objeżdżamy tak, jak P'Q'R', a na koniec wracamy z P''Q''R'' do PQR przez przesunięcie odwrotne.

Podobnie można uzasadnić całkiem ogólne twierdzenie.

Twierdzenie 3'.  
Niech figury F, F' można nałożyć na siebie pewnym ruchem na płaszczyźnie. Jeśli F i F' leżą w wypukłej figurze G, to jeśli F' jest obracalna w G, to F jest też obracalna w G.

Zobaczmy, jaki ruch mogą wykonywać trójkąty równoboczne obracalne w trójkącie ABC. Przykład widać na poniższym rysunku. Oczywiście są też inne sposoby zawracania trójkątów.

Zauważmy, że każdy trójkąt ma jakiś kąt nie większy niż 60^o, zatem każdy trójkąt równoboczny, obracalny w ABC, można przemieszczać tak, jak na powyższym rysunku (patrz Twierdzenie 3).

Nasuwa się naturalne pytanie:

Twierdzenie 2 mówi, że nie są większe od najmniejszego trójkąta równobocznego dotykającego wszystkich boków trójkąta ABC. Jak zatem wygląda najmniejszy trójkąt równoboczny dotykający wszystkich boków ABC? Mówi o tym następujące twierdzenie.

Twierdzenie 4.  
Niech dany będzie trójkąt ostrokątny ABC i niech trójkąt równoboczny P₀Q₀R₀ będzie najmniejszym z trójkątów równobocznych dotykających wszystkich boków trójkąta ABC.
Wtedy:

a)  Trójkąt P₀Q₀R sub>0 ma boki długości

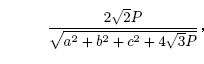
przy standardowych oznaczeniach,
tzn. a, b, c - długości boków, P - pole trójkąta ABC.

b)  Trójkąt P₀Q₀R₀ jest obracalny w obrębie trójkąta ABC.
Jest największym trójkątem równobocznym, obracalnym w ABC.

c)  Proste prostopadłe do boków trójkąta ABC, wystawione w punktach P₀, Q₀, R₀, przecinają się w jednym punkcie.

d)  Proste prostopadłe do boków trójkąta P₀Q₀R₀, przechodzące przez punkty A, B, C, przecinają się w jednym punkcie T.
Punkt T nazywa się "punktem Torricellego" i ma następujące własności:
- kąty ATB, BTC, CTA mają po 120^o,
- AX+BX+CX jest najmniejsze dla X=T.

e)  Boki trójkąta P₀Q₀R₀ są równoległe do boków trójkąta wyznaczonego przez środki trójkątów równobocznych, zbudowanych na bokach trójkąta ABC (na zewnątrz tego trójkąta).

Dowód powyższego twierdzenie jest dość trudny. W przypadku, gdy trójkąt ABC nie jest ostrokątny, uogólnienie twierdzenia 4 nie jest natychmiastowe - wymaga dodatkowych obserwacji. Jeszcze trudniejsze wydają się następujące problemy.

Problem 1.  
Niech trójkąt równoboczny PQR będzie obracalny w obrębie trójkąta ABC. Czy obracalność PQR można zrealizować przez ruch, będący 'kombinacją' obrotów i przesunięć?

Problem 1'.  
Niech figura F będzie obracalna w obrębie wypukłego wielokąta W. Czy obracalność F można zrealizować przez ruch, będący 'kombinacją' obrotów i przesunięć?

Problem 1''.  
Niech figura F będzie obracalna w obrębie figury wypukłej W. Czy obracalność F można zrealizować przez ruch, będący 'kombinacją' obrotów i przesunięć?

Problem 2.  
Niech trójkąt nierównoboczny PQR będzie obracalny w obrębie trójkąta ABC. Czy trójkąt P'Q'R', przystający do PQR i zawarty w ABC jest obracalny w ABC?

Problem 2'.  
Niech figura F będzie obracalna w obrębie figury wypukłej G. Czy każda figura F' przystająca do F i zawarta w G jest obracalna w G ?