Strona główna › MAT-ŚWIAT

Odlotowe figury


Redaktor działu:
Krzysztof Omiljanowski (komil(at)math.uni.wroc.pl)
pracownik IM UWr


Z jednej siatki

Czy z jednej siatki można skleić dwa różne wielościany? Oczywiście że tak. Pewne części siatki możemy bowiem skleić "na wypukło" lub "na wklęsło". Ale czy jest to możliwe, jeśli otrzymane z jednej siatki wielościany mają być wypukłe?

Czytaj dalej


Bryły platońskie z uzdą

Modele wielościanów platońskich wklejone do zeszytu i zawsze pod ręką? To możliwe. Wystarczy ich siatki przykleić na kartce jedną ścianką, wykonać kilka dziurek, przepleść nitkę i dzięki temu wyposażyć modele w specjalne uzdy do ściągania.

Czytaj dalej


Samowstający dwunastościan

Do zbudowania modelu potrzebujemy siatkę 12-ścianu foremnego rozciętą na dwie przystające części oraz gumkę recepturkę. Model można przechowywać na płasko między kartkami zeszytu, a kiedy zajdzie potrzeba, sam przybierze formę trójwymiarową. 

Czytaj dalej


Koła w narożach

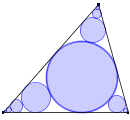W każdy trójkąt można wpisać koło. W powstałe naroża dalej można wpisywać kolejne koła. Jak jest suma pól tych kół? Czy jest jednakowa dla wszystkich trójkątów o tym samym polu? Sprawdźmy.
Czytaj dalej


Odcinek paraboli (z cyklu 'Śladami Archimedesa')

Już Archimedes potrafił obliczyć pole odcinka paraboli. Archimedes nie rachował, jego rozumowanie było geometryczne. Tu pokażemy, jak rachunek algebraiczny może zastąpić rozumowanie geometryczne. Ponadto pokażemy uogólnienie dla linii y = x3.

Czytaj dalej
« pierwsza‹ poprzednia123456789…następna ›ostatnia »


Spis treści działu

Tytuł Autor Data
Kopalnia metodStefan Mizia2020.12.01
Kosmiczny wzór na pole trójkątaStefan Mizia2020.11.27
Piramida Sierpińskiegoopracowanie redakcyjne2019.11.26
Z siatki sześcianuopracowanie redakcyjne2019.11.21
Fleksoryopracowanie redakcyjne2019.11.21
Z jednej siatkiopracowanie redakcyjne2019.11.19
Bryły platońskie z uzdąopracowanie redakcyjne2019.11.15
Samowstający dwunastościanopracowanie redakcyjne2019.11.13
Koła w narożachKrzysztof Omiljanowski2016.11.28
Odcinek paraboli (z cyklu 'Śladami Archimedesa')Krzysztof Omiljanowski2015.05.14
Wytoczone sercaKrzysztof Omiljanowski2015.03.19
W puszce pod piłkąKrzysztof Omiljanowski2014.10.05
Kule w ośmiościanie foremnymKrzysztof Omiljanowski2014.09.09
WianuszkiKrzysztof Omiljanowski2014.07.27
Stożek w klatkachKrzysztof Omiljanowski2014.07.24
Średnia długości przekątnychKrzysztof Omiljanowski2014.01.27
Średnia długości przekątnych (tylko dla dorosłych)Krzysztof Omiljanowski2014.01.26
Trójkąty Reuleaux 3DKrzysztof Omiljanowski2013.01.31
Środki figur płaskichKrzysztof Omiljanowski2013.01.09
Odcinek figurKrzysztof Omiljanowski2012.12.06
Bryły z kreskowaną okrągłą podstawąKrzysztof Omiljanowski2012.09.30
O dziale (hiperbolicznie)Krzysztof Omiljanowski2012.05.31
O dziale (platonicznie)Krzysztof Omiljanowski2012.05.30
Im więcej, tym... gorzej?Krzysztof Omiljanowski2012.04.30
Kulą w... stożekKrzysztof Omiljanowski2012.04.30
B(a)ryłka ArchimedesaKrzysztof Omiljanowski 2012.04.29
Bańki w sześcianie i w komputerzeKrzysztof Omiljanowski2011.12.30
[3, 4, 5] w 3DKrzysztof Omiljanowski2011.12.27
Kula w szkielecieKrzysztof Omiljanowski2011.12.23
Sześcian z sześciu deseczekKrzysztof Omiljanowski2011.10.31
Rolling conesKrzystzof Omiljanowski2011.07.31
Ile ma podstaw?Krzysztof Omiljanowski2011.05.26
Wigwamy jak stożkiKrzysztof Omiljanowski2011.04.30
Czy wstęgę Möbiusa można zrobić z paska papieru? (1)Krzysztof Omiljanowski2011.01.28
Grube punktyKrzysztof Omiljanowski2010.12.14
Klasyfikacja 'wklęsłych trójkątów'?Krzysztof Omiljanowski2010.12.13
K-kładkiKrzysztof Omiljanowski2010.11.26
Szachownica na ZiemiKrzysztof Omiljanowski2010.10.30
Kłopoty z obwodemKrzysztof Omiljanowski2010.09.30
Zawracanie trójkątaKrzysztof Omiljanowski2010.07.30
Na skróty - z niespodziankamiKrzysztof Omiljanowski2010.07.08
W obrębie trójkątaKrzysztof Omiljanowski2010.06.24
Pakowanie trzech kwadratówKrzysztof Omiljanowski2010.06.13
StożsłupyKrzysztof Omiljanowski2010.05.01
Klin ze stożkaKrzysztof Omiljanowski2010.03.31
Klina klinemKrzysztof Omiljanowski2010.02.22
Bałwan jaki jest, każdy widzi... inaczejKrzysztof Omiljanowski2010.02.06
Wszystkie połowiące obwód trójkątaKrzysztof Omiljanowski2010.01.24
Wszystkie połowiące pole trójkątaKrzysztof Omiljanowski2010.01.16
Domino - jak leciKrzysztof Omiljanowski2009.12.31
Symetryzacja SteineraKrzysztof Omiljanowski2009.12.20
Poprawianie Archimedesa?Krzysztof Omiljanowski2009.11.24
Anatomia gwiazdKrzysztof Omiljanowski2009.10.31
Siła wektorów (i geometrii)Krzysztof Omiljanowski2009.10.26
Domino - jak leży?Krzysztof Omiljanowski2009.10.11
Pinezką i palcemKrzysztof Omiljanowski2009.09.15
Z pinezką - rzeczywistą i urojonąKrzysztof Omiljanowski2009.08.12
Puszka pod kloszemKrzysztof Omiljanowski2009.07.10
Puszka pod namiotemKrzysztof Omiljanowski2009.07.05
Puszka w koszuKrzysztof Omiljanowski2009.06.25
Wielobok środków - uogólnieniaKrzysztof Omiljanowski2009.06.21
Wielobok środków - iteracjeKrzysztof Omiljanowski2009.06.01
Wielobok środków - podobieństwoKrzysztof Omiljanowski2009.05.25
Jakie wieloboki są wielobokami środków?Krzysztof Omiljanowski2009.05.12
Wielobok środków - pola i obwodyKrzysztof Omiljanowski2009.04.17
Równoległościan? Może tak, może nie...Krzysztof Omiljanowski2009.03.26
Na zakręcieKrzysztof Omiljanowski2009.01.04
Zoom, zoom, zoom... i twierdzeniaKrzysztof Omiljanowski2008.11.13
Zoom, zoom, zoom,...Krzysztof Omiljanowski2008.09.09
Studnia egipska (3) - Wersja 3DKrzysztof Omiljanowski2008.03.17
Studnia egipska (2) - Między prawdą a mitemKrzysztof Omiljanowski2008.03.04
Zakręcone graniastosłupy (2) - Dodatkowo pokręconeKrzysztof Omiljanowski2008.02.15
Zakręcone graniastosłupy (1)Krzysztof Omiljanowski2008.02.11
Prostokrąg (2) - Wpisany w prostokątKrzysztof Omiljanowski2007.10.30
Prostokrąg (1)Krzysztof Omiljanowski2007.09.30
Rolling Stones (4) - Matematyczne wybojeKrzysztof Omiljanowski2007.09.21
Rolling Stones (3) - Rysują cykloidęKrzysztof Omiljanowski2007.09.17
Rolling Stones (2) - Polygon RoverKrzysztof Omiljanowski2007.09.15
Rolling Stones (1)Krzysztof Omiljanowski2007.09.13


Powrót na górę strony