 Na skróty - to zrozumiałe dla każdego wytrawnego turysty. Ale jakie mogą nas tu czekać niespodzianki? Zobacz. Rzecz dotyczy deptania trawników, które chociaż prawnie nie jest już zabronione, bywa nieeleganckie i szkodliwe ekologicznie. Matematyk potrafi jednak podeptać trawnik optymalnie.
Na skróty - to zrozumiałe dla każdego wytrawnego turysty. Ale jakie mogą nas tu czekać niespodzianki? Zobacz. Rzecz dotyczy deptania trawników, które chociaż prawnie nie jest już zabronione, bywa nieeleganckie i szkodliwe ekologicznie. Matematyk potrafi jednak podeptać trawnik optymalnie.
Odlotowe figury
Na skróty - z niespodziankami
W obrębie trójkąta
 Gdy na bokach trójkąta ABC leżą wierzchołki drugiego trójkąta PQR, to ABC blokuje PQR i zabezpiecza ten wewnętrzny trójkąt przed przesunięciem. Mimo tego zazwyczaj trójkąt PQR ma trochę luzu i może się przemieszczać. Zobacz jak. Wcześniej warto przeczytać artykuł Pakowanie trzech kwadratów.
Gdy na bokach trójkąta ABC leżą wierzchołki drugiego trójkąta PQR, to ABC blokuje PQR i zabezpiecza ten wewnętrzny trójkąt przed przesunięciem. Mimo tego zazwyczaj trójkąt PQR ma trochę luzu i może się przemieszczać. Zobacz jak. Wcześniej warto przeczytać artykuł Pakowanie trzech kwadratów.
Pakowanie trzech kwadratów
 W trójkąt równoboczny można zapakować trzy jednakowe kwadraty i to na wiele sposobów. W artykule przedstawiamy kilka takich możliwości. Czy są wśród nich takie, które zabezpieczają kwadraty przed przemieszczaniem się? Zobacz. Zbadaj inne rozwiązania tego problemu.
W trójkąt równoboczny można zapakować trzy jednakowe kwadraty i to na wiele sposobów. W artykule przedstawiamy kilka takich możliwości. Czy są wśród nich takie, które zabezpieczają kwadraty przed przemieszczaniem się? Zobacz. Zbadaj inne rozwiązania tego problemu.
Stożsłupy
 W matematyce nazwa 'stożsłup' nie istnieje. Pojęcie to powstało na potrzeby naszego tego artykułu. Stożsłupy to klasa brył zawierająca stożki i ostrosłupy. Jakie wspólne cechy mają te figury? Po co wprowadzać takie pojęcie? Zobacz.
W matematyce nazwa 'stożsłup' nie istnieje. Pojęcie to powstało na potrzeby naszego tego artykułu. Stożsłupy to klasa brył zawierająca stożki i ostrosłupy. Jakie wspólne cechy mają te figury? Po co wprowadzać takie pojęcie? Zobacz.
Klin ze stożka
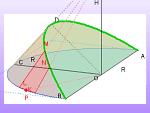 Sposobem na obliczanie objętości klinów wyciętych z walca okazało się podzielenie ich na mniejsze kliny (zajrzyj koniecznie do artykułu Klina klinem). Czy jest to dobra metoda także dla klinów wyciętych ze stożka? Sprawdź!
Sposobem na obliczanie objętości klinów wyciętych z walca okazało się podzielenie ich na mniejsze kliny (zajrzyj koniecznie do artykułu Klina klinem). Czy jest to dobra metoda także dla klinów wyciętych ze stożka? Sprawdź!







