Zad. 1. Pewna liczba niejednocyfrowa, ale mająca co najwyżej cztery cyfry, ma tę własność, że jest równa sumie silni swoich cyfr. Co to za liczba? Przypominamy, że n! = 1⋅2⋅...⋅(n−1)⋅n dla n≥1, a 0!=1.
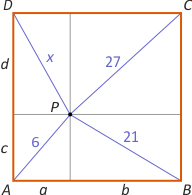
Zad. 2. Punkt P leży wewnątrz kwadratu ABCD. Odległości tego punktu od wierzchołków A, B i C wynoszą odpowiednio 6, 21 i 27. Ile wynosi odległość punktu P od wierzchołka D?
Zad. 3. Ile nieparzystych dzielników ma liczba 20202020?
W marcu punkty zdobyli:
- 3 pkt. –Ewa Bogacz SP 76 Wrocław, Artur Bumażnik SP 1 Piechowice, Emilia Cichowska SP 14 Lubin, Paweł Czarny SP 36 Wrocław, Łukasz Ganczarek SP 10 Wrocław, Paulina Hołodniuk SP 2 Wołów, Maja Jas SP 5 Strzelin, Filip Klich SP Ekola Wrocław, Klara Kogut SP 9 Gliwice, Szymon Kuźniar SP Ciechanów, Maya Małachowska SP 3 Głogów, Julia Marcinkowska SP 11 Inowrocław, Paweł Michałowski SP 1 Białystok, Weronika Michałowska SP 1 Białystok, Julita Masłowska SP 3 Głogów, Miłosz Popowicz SP 91 Wrocław, Karol Skowera SP 2 Wałbrzych, Karol Szaniewski SP 16 Studzienice, Weronika Tracz SP Stare Bogaczowice, Franciszek Zakrawacz SP2 Wałbrzych, Miłosz Zakrzewski SP Gostycyn, Oksana Zatwardnicka SP 28 Wałbrzych;
- 2,5 pkt. –Nadia Stefanowska SP 10 Legnica, Alicja Szwarczyńska SP Kowalowa;
- 2 pkt. – Patryk Boruń SP 9 Wałbrzych, Jakub Dudek SP 11 Inowrocław, Martyna Gruszczyńska SP 19 Gliwice, Kacper Kazik SP 4 Inowrocław, Miłosz Kiełbasa SP 2 Tomaszów Lubelski, Maja Muszyńska SP Jedlnia-Letnisko, Sandra Łuczak SP 107 Wrocław, Maja Kiraga SP Jedlnia-Letnisko, Agnieszka Płudowska SP 18 Wrocław Lublin, Maja Skuza SP 5 Kielce, Tymon Srokosz SP 52 Warszawa, Filip Timofiejczuk SP 3 Tarnowskie Góry;
- 1 pkt. – Aleksandra Antonowicz SP 28 Wałbrzych, Zuzanna Basińska SP 11 Inowrocław, Olga Bazelska SP 11 Inowrocław, Kaja Madej SP Józefowo nad Wisłą.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Jedyną liczbą o tej własności jest 145 = 1!+4!+5! = 1+24+120. Wiemy, że 0! = 1, 1! = 1 i można obliczyć, że 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! = 720, 7! = 5040, 8! = 40320, a to jest już liczba pięciocyfrowa, więc za duża na warunki zadania.
a) Przypuśćmy, że szukana liczba jest dwucyfrowa. Nie może w niej występować cyfra większa niż 4, bo silnia takiej liczby jest co najmniej trzycyfrowa. Nie mogą też w niej występować wyłącznie cyfry mniejsze niż 4, bo suma ich silni jest jednocyfrowa (z wyjątkiem liczby 33, ale ona nie spełnia warunków zadania). Liczby wymagające rozważenia to 14, 24, 34 i 44, ale żadna z nich nie spełnia warunków zadania.
b) Przypuśćmy, że szukana liczba jest trzycyfrowa. Nie może w niej występować cyfra większa od 6, bo silnia takiej liczby jest co najmniej czterocyfrowa. Nie może w niej też występować 6, bo 6! = 720, więc w szukanej liczbie występowałaby jednak cyfra większa od 6. Musi się w niej pojawić 5, bo 4!+4!+4! = 72, a to jest dwucyfrowe. Cyfra 5 nie stać na miejscu setek, bo wtedy nawet gdyby w liczbie były tylko cyfry 5, to suma ich silni byłaby mniejsza od 500. Gdyby w liczbie były dwie cyfry 5, to musiałaby się ona zaczynać od 2 (bo wtedy suma silni to 2·120 + liczba nie większą od 24), ale liczba 255 nie spełnia warunków zadania. Cyfra 5 jest zatem jedna, a cyfrą setek musi być 1 (dlaczego?). Liczby wymagające rozważenia to 151, 152, 153, 154 oraz 115, 125, 135 i 145, ale tylko ta ostatnia spełnia warunki zadania.
c) Przypuśćmy, że szukana liczba jest trzycyfrowa. Analizę przypadków, która pokazuje, że nie ma liczby czterocyfrowej o szukanych własnościach, pozostawiamy czytelnikom.
Zad. 2. Długość PD wynosi 18. Narysujmy odcinki równoległe do boków kwadratu przechodzące przez punkt P i oznaczmy długości odcinków powstałych na bokach kwadratu przez a, b, c i d, a długość PD przez x. Na mocy twierdzenia Pitagorasa otrzymujemy równości: a2+c2 = 62, b2+c2 = 212, b2+d2 = 272 i a2+d2 = x2. Po dodaniu stronami pierwszego i trzeciego równania po lewej stronie otrzymujemy a2+b2+c2+d2, podobnie po dodaniu stronami drugiego i czwartego równania. Mamy zatem a2+b2+c2+d2 = 62+272 = 212+x2, skąd x2 = 36+729−441 = 324, a więc x = 18.
Zad. 3. Liczba 20202020 ma 4084441 dzielników nieparzystych. Rozłóżmy ją na czynniki pierwsze. Mamy (22⋅5⋅101)2020 = 24040⋅52020⋅1012020. Dzielnik tej liczby jest postaci 2m⋅5k⋅101n, przy czym 0≤m≤4040, 0≤k≤2020 i 0≤n≤2020. W naszym przypadku m=0, bo inaczej dzielnik byłby parzysty. Liczb postaci 5k⋅101n, gdzie k i n przyjmują niezależnie wartości od 0 do 2020, jest 2021⋅2021 = 4084441 (gdy k=0 i n=0, to otrzymujemy liczbę 50⋅1010 = 1, która jest oczywiście nieparzystym dzielnikiem każdej liczby).








Nie po kolei
Marzec są rozwiązania, luty nawet rozwiązań nie ma, a co dopiero wyniki... Chronologia zaczerpnięta z "Wehikułu czasu"?
Z nadzieją...
Zgadzam się. Ten konkurs to świetna inicjatywa dla naszych zdolnych uczniów, natomiast brak wyników od lutego, gdy jest połowa maja, to troszkę brak szacunku dla uczestników i niestety gaszenie ich entuzjazmu z jakim rozpoczynali. Nadzór nad Ligą to z pewnością ogrom pracy i poświęconego czasu, ale nadzieja nie gaśnie, że dzieci doczekają. Pozdrawiam.