W sztuce origami wyróżnia się rozmaite bazy, czyli formy podstawowe - początkowe ciągi zagięć wspólnych dla wielu figur. Klasycznym przykładem jest baza żuraw, której diagram stanowi około 2/3 diagramu pełnego żurawia, ale jest też początkowym krokiem do budowania innych, bardziej skomplikowanych modeli, np. sowy, łabędzia czy nietoperza.
W artykule pokazujemy, jak przygotować dwie podstawowe, wzajemnie dualne bazy origamiczne - kwadratu i trójkąta - oraz jak wykorzystać je do zbudowania modułu, za pomocą którego można wykonać modele różnych wielościanów.
Baza trójkąt była już opisana w artykule Ośmiościan dla leniwych. Baza kwadrat jest do niej dualna. Można myśleć, że powstaje przez wywracanie na lewą stronę. Zanim przystąpimy do konstruowania modułu, przypomnijmy, jak wykonuje się obie wspomniane bazy.
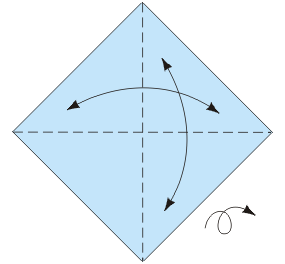
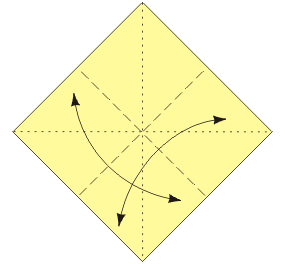
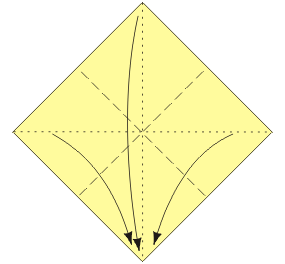
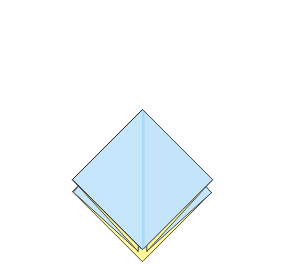

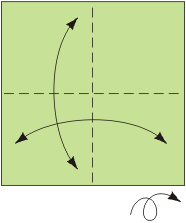
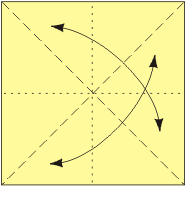

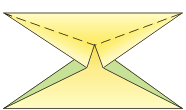
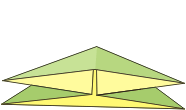
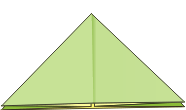
Z bazy kwadrat i trójkąt można złożyć ciekawy moduł poprzez nałożenie pierwszej z nich na drugą i zagięcie do środka wystających „rogów” bazy kwadrat. Moduł ten został zaprojektowany przez Lewisa Simona i nazwany żyroskopem (gyrocsope). Jest modułem wierzchołkowym, to znaczy, że elementów trzeba złożyć tyle, ile wierzchołków ma składana bryła.



Z modułu Simona można składać niemal wszystkie wielościany, w których wierzchołkach schodzą się 4 krawędzie. Poszczególne części łączy się poprzez wsuwanie rogu jednego modułu w róg drugiego.


W ten sposób możemy uzyskać np. ośmiościan foremny, sześcio-ośmiościan czy sześcio-ośmiościan rombowy mały (ale nie czworościan - kąt modułu jest zbyt duży). Dla ułatwienia pracy podczas dokładania nowych modułów można te już sczepione ustabilizować spinaczami, które na koniec należy usunąć.




Jeśli moduły bazowe dodatkowo pozaginamy w miejscach łączenia, uzyskamy modele o wdzięcznym wyglądzie.


Moduł Simona można też wykorzystać do budowania wielościanów kręciołkowych, opisanych w innym artykule. Powstają wtedy bardzo atrakcyjne modele.
Tu będą zdjęcia
W analogiczny sposób co moduł Simona można przygotować moduły z kartek trójkątnych lub pięciokątnych. Wtedy mamy możliwość budowania wielu nowych brył (wielościanów, w których wierzchołkach schodzą się trzy krawędzie lub pięć krawędzi). Z pierwszych da się wykonać np. sześcian lub dwunastościan foremny (zdjęcie niżej), a z drugich np. dwudziestościan foremny. Moduły różnych typów można łączyć ze sobą nawzajem, budując wielościany mające jednocześnie wierzchołki różnych stopni (3, 4, lub 5).
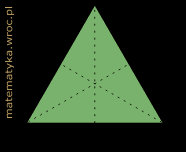
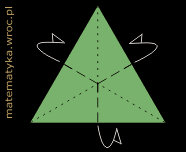

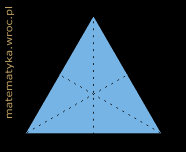
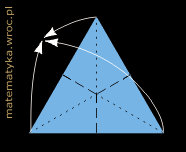

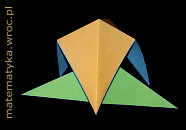


Przykładowe modele brył zbudowane z takich modułów widać na zdjęciach poniżej.
 Dwunastościan foremny z modułu trójkątnego.
Dwunastościan foremny z modułu trójkątnego.
Bibliografia
- http://www.origami.art.pl/bazy.php
- http://www.youtube.com/watch?v=nUziQd6Cj9I
- http://www.origamee.net/







Jak duży sześcian w ośmiościanie?
Warto również wspomnieć, iż w takim modelu ośmiościanu foremnego można się dopatrzeć faktu, że sześcian i ośmiościan foremny są bryłami dualnymi.
Na zdjęciu sześcian wykonany jest w technice sonobe.
Uwaga, nagroda!
Pozdrowienia dla redaktorów Portalu:)
Czyżby szukany stosunek był równy √2-1?
Tak jest
Czy coś ciekawego, gdy wywrócimy na lewą?
A próbował ktoś wywracać na lewą stronę? Czy każdy z powyższych modeli się da? Co uzyskamy po takim przekształceniu modeli ze zdjęć powyżej (tych, które się da)?
Warto najpierw powywracać na lewą stronę we własnej wyobraźni, a później próbować w realu. Może przydać się klej. Pewnie zaburzy to zasady origami, ale nie odbierze frajdy ze składania.
Zadanie
Nagroda
Tradycyjnie redakcja Portalu funduje nagrodę-niespodziankę, za pierwszą poprawną odpowiedź na postawione wyżej pytanie. Nagrodę otrzymuje też Piotr - autor pytania - nauczyciel matematyki.
Trzy razy to, co wcześniej
Czy ten stosunek wynosi może [tex]3(\sqrt{2}-1)[/tex]?
Niedobrze
Niestety ta odpowiedź nie jest właściwa.
Podpowiedź: 1/3 wysokości trójkątnej kartki ma być równa połowie boku kwadratowej, kolejny krok to przedstawienie długości boku trójkąta za pomocą długości boku kwadratowej kartki i już mamy szukany stosunek... Powodzenia!
Nie rozumiem
Jeżeli podążymy za podpowiedzią wyżej, to stykające się krawędzie wierzchnich karteczek z modułów trójkątnego i kwadratowego (gdy oczywiście te moduły połączymy) będą różnej długości. Wtedy te moduły chyba nie będą za bardzo pasowały? Wydaje mi się ponadto, że nieważne jak długie będą "rogi", które wkładamy do środka przy łączeniu modułów (bo chyba na tym opierał się pomysłm podanej wskazówki). Dalej pozostaję przy mojej wcześniej udzielonej odpowiedzi. Chyba, że źle rozumiem to pytanie.
Wg mnie jest poprawna
Uważam, że podana odpowiedź na moje pytanie jest poprawna, a wskazówka Sylwii prowadzi na manowce. Może niezbyt precyzyjne było sformułowanie
problemu. "Pasuje" oznacza wg mnie, że po włożeniu jednego modułu w drugi nic nie będzie odstawać. Sprowadza się to do tego, że bok sześciokąta, który powstaje po nałożeniu jednego trójkąta na drugi musi mieć tę samą długość, co bok ośmiokąta, który powstaje po nałożeniu jednego kwadratu na drugi, czyli gdy bok trójkąta jest równy a, a kwadratu b, to
1/3 a = b(√2-1).
Trzeba doprecyzować
Pojęcie "pasowania" modułów do siebie jest mylące. Ja rozumiem to tak, że wielkość obu modułów jest identyczna, a wtedy stosunek boków trójkąta i kwadratu jest równy √3. Natomiast jeśli "kieszonki", do których wsuwamy moduły, mają mieć taką samą wielkość (a o to chodziło Piotrowi), to faktycznie odpowiedź 3(√2 -1) jest OK.
W pytaniu Piotra jest też haczyk (o którym wspomina Anonimowy), bo końcówki modułu trójkątnego będą wtedy za długie, aby wsunąć je do modułu kwadratowego, tzn. kieszonki będą odpowiedniej wielkości, ale cały moduł będzie za duży, aby go umieścić w drugim ;)
Nic nie jest za długie
Nic nie jest za długie. Wszystko ładnie pasuje. Można się o tym przekonać, wykonując dwa moduły i łącząc je, albo przeprowadzając odpowiednie rachunki. Długość końcówki modułu trójkątnego to 1/3 wysokości trójkąta o boku a, czyli ok. 0,28a. Natomiast głębokość kieszonki to ok. 0,4a.
Dziękuję
Jasne że pasuje! Dziękuję Piotrowi za czujność i sprawdzenie moich rachunków... Co te ferie robią człowiekowi z intelektem... Pozdrawiam serdecznie!
Zaliczone
Uogólnienie
Spróbujmy zatem uogólnić postawiony wcześniej problem. Rozważmy dwa moduły Simona złożone z karteczek w kształcie n-kąta foremnego i m-kąta foremnego (n≠m). Jaki musi być stosunek długości boków karteczki n-kątnej do m-kątnej, aby moduły z nich zbudowane pasowały do siebie nawzajem (w rozumieniu Piotra)?
Ma się rozumieć
Rzecz jasna, redakcja WPM tradycyjnie ufunduje ciekawą nagrodę za poprawną odpowiedź.
Szukany stosunek
Szukany stosunek boków w pytaniu Anonimowego to
tgα·tgβ/2 ÷ tgβ·tgα/2, gdzie α=π/n i β=π/m?
Jest OK
Też mi tak wyszło.
Pytanie o ograniczenia
Istnieją pewne ograniczenia w możliwości wykorzystania tego typu modułów, np. z modułów o czterech ramionach nie da się wykonać dwudziesto-dwunastościanu, mimo że w jego wierzchołkach schodzą się po 4 krawędzie. Podobnie z modułów trójkątnych nie da się zbudować czworościanu foremnego, choć w jego wierzchołkach spotykają się 3 krawędzie. Pytanie szczególne: dlaczego tak jest? Pytanie ogólne: jakie są ograniczenia dla tego typu modułów i skąd się one biorą?
Za duże kąty
Moduły mają za duże kąty, np. ten trójkątny ma kąty na tyle duże, że nie da się go "wcisnąć" w narożnik czworościanu, którego kąty (bryłowe) są stosunkowo małe. Nie umiem tego dokładnie wyliczyć, ale na pewno na tym to polega.
Mała modyfikacja i czworościan jest!