W magicznym zwierciadle Eschera

Czy matematyka może stać się natchnieniem dla artysty? Czy może stać się narzędziem pomagającym przekazać myśli i idee zrodzone w naszym umyśle? Najpełniej swoją twórczością odpowiedział na to pytanie Maurits Cornelis Escher (1898-1972) - holenderski grafik o wyjątkowej wyobraźni geometrycznej, przedstawiciel op-artu, najbardziej znany artysta w świecie nauki.

Jego twórczość stała się tematem licznych artykułów z różnych dziedzin: matematyki, psychologii, historii sztuki oraz popularyzacji nauki. Wystawa dzieł Eschera towarzyszyła Międzynarodowemu Kongresowi Matematyków w Amsterdamie w 1954 roku. Jego twórczość,  przemawiając językiem matematyki, do dziś  kształtuje wyobraźnię plastyków, grafików komputerowych, filmowców i pasjonatów matematyki.

Czego możemy nauczyć się, idąc śladami Eschera? Poniżej przedstawiamy ogólne spojrzenie na sztukę tego artysty, koncentrując się głównie na odkrywaniu w niej różnych matematycznych inspiracji.

Zamieszczone w artykule grafiki pochodzą ze strony Fundacji Eschera (www.mcescher.com) z siedzibą w jego rodzinnym mieście Baarn w Holandii. Na tej stronie można znaleźć bogatą kolekcję obrazów artysty. Zapraszamy do jej odwiedzenia. A tutaj prezentujemy materiał dotyczący Muzeum Eschera w Hadze.

Jest to zapewne najbardziej kuriozalne dzieło, absolutnie niepowtarzalne, jakiego żaden inny artysta grafik na świecie (z całym szacunkiem) Ci nie zaprezentuje. Nie brzmi to zbyt skromnie, ale cóż na to poradzę. Takie to właśnie jest. Tak pisał Escher o swojej sztuce w liście do przyjaciela. Nie ma w tym zdaniu żadnej przesady, bo wyjątkowość jego obrazów jest oczywista nawet dla mało wprawnych odbiorców.

Spójrzmy na jeden z najbardziej znanych drzeworytów tego artysty - "Wstęga Möbiusa" (1963). W pewnym sensie charakteryzuje on całą jego twórczość. W jednym z listów do syna George’a z 1961 roku czytamy: Wciąż próbuję skończyć z rysowaniem. Ale stanowczo sprzeciwia się temu wstęga Mobiusa przyczajona w mojej duszy. Ciągle i wszędzie słyszę pełną żalu prośbę: chcę stąd wyjść! Jakże często wstęga Möbiusa okazuje się metaforą także naszych działań i naszej rzeczywistości (inne przykłady wykorzystania wstęgi Möbiusa w sztuce znajdziesz na Portalu tutaj, a w życiu codziennym - także tutaj).

Sztuka Eschera ukazuje względność i subiektywność naszego postrzegania. Stawia pytanie, na ile możemy wierzyć naszym zmysłom, odzwierciedla dualizm naszej rzeczywistości - jej harmonię przy jednoczesnym całkowitym braku uporządkowania, jej ograniczenie z jednoczesną perspektywą nieskończoności, jej powtarzalność, a jednocześnie nieprzewidywalność. Spójrzmy na litografię "Porządek i chaos" (1950). Jej sens jest bardzo czytelny. Regularny dwunastościan gwiaździsty wyłaniający się z kuli symbolizującej harmonię wkomponowane są w chaos codzienności. Żyjemy w idealnie uporządkowanym świecie, chociaż to, co z niego na co dzień postrzegamy, często świadczy, że jest inaczej.

Porządek i chaos - litografia, 1950

Escher proponuje widzowi zabawę architekturą, perspektywą i przestrzenią. W jego pracach odnajdujemy intrygującą rzeczywistość pełną sprzeczności i fantazji, absurdalnego poczucia humoru, ale i matematycznej logiki. Prezentując swoje fantastyczne wizje, artysta zawsze kieruje się żelaznymi zasadami matematyki, które rzadko kojarzymy z prawami estetyki. To właśnie matematyka jest dla niego głównym środkiem wizualnego przedstawienia wyobrażeń o rzeczywistości. Ukazuje ją w różnych perspektywach, świetnie wykorzystując zasady rzutu środkowego i równoległego, zaskakując niezwykłymi rozwiązaniami geometrycznymi w różnych wymiarach i w różnych geometriach, które jednak bazują zawsze na szczegółowych szkicach i matematycznych obliczeniach.

Sztuka Eschera nie wymaga od odbiorcy wiedzy matematycznej, ale znajomość rządzących nią reguł pozwala na jej pełniejszy odbiór i na podjęcie tej nieco przewrotnej zabawy z autorem podczas prób rozszyfrowania matematycznych inspiracji jego dzieł. Przyglądając się im dokładniej i analizując z punktu widzenia matematyka, dostrzegamy nie tylko piękno matematycznych obiektów, ale i głębię ukrytych za nimi treści i znaczeń.

Za "sztukę matematyczną" powszechnie przyjmuje się dzieła, które wykazują matematyczną strukturę i oddziaływują matematycznymi skojarzeniami na wyobraźnię matematyków. Odróżnia się w niej (za chińskim matematykiem Xah Lee) sztukę ilustrującą matematyczne koncepcje i sztukę, która jest inspirowana matematyką.

Dorobek Eschera charakteryzuje bogactwo egzemplifikacji obydwu tych nurtów. Wiele w nim artystycznych wizji matematycznych koncepcji i obiektów, ale i prac pozornie z matematyką nie związanych, jednak wyraźnie bazujących na jej ideach. Do pierwszej grupy należą niezwykłej urody przedstawienia wielościanów, pierścieni, spiral czy węzłów, a do drugiej - tajemnicze odbicia w niezwykłych lustrzanych taflach.

"Gwiazdy" – drzeworyt sztorcowy, 1948	"Wiry" – drzeworyt sztorcowy, 1957	"Sferyczne spirale" – drzeworyt langowy, 1958

"Węzły" – drzeworyt langowy, 1965	"Grawitacja" - litografia, 1952	"Ręka z odbiciem w kuli" - litografia, 1935

	"Martwa natura ze sferą" - litografia, 1934

Poznajmy kolejne przykłady matematycznych konceptów widzianych oczyma Echera.

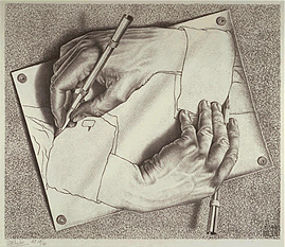
Ulubionym motywem Eschera są niezwykłe metamorfozy, w których odbiorze łatwo się zagubić. Widz traci orientację w przestrzeni, nie wie, gdzie jest podłoga, ściana, a gdzie sufit, co jest wklęsłe, a co wypukłe i czym w istocie jest dany kształt. W jego pracach znajdujemy zdumiewające zestawienia płaszczyzny i przestrzeni oraz próby usunięcia granicy między nimi (np. gdy ręka rysuje rękę rysującą tę właśnie rękę lub gdy z płaskiego rysunku nagle wyłaniają się żywe, trójwymiarowe stworzenia).

"Rysujące ręce" – litografia, 1948	"Gady" – litografia, 1943

Z tych dzieł emanuje uporczywe dążenie do osiągnięcia matematycznej precyzji, którą autor uważał za niedościgłą. O swojej popularnej litografii "Belweder" powiedział: Ten rysunek nie zasłużył sobie na wysoką ocenę. Jak przypuszczam dlatego, że zrezygnowałem w nim z matematycznej dyscypliny. Zdaniem matematyków moje i ich królestwa sąsiadują ze sobą, ale się nie pokrywają. Szkoda!
	"Belweder" – litografia, 1958	"Cykl" – litografia, 1938

Innym szczególnym obszarem zainteresowań Eschera stały się tesselacje (od ang. tessellation), czyli parkietaże płaszczyzny lub posadzki.  Artysta tak pisał w liście do bratanka w 1944 roku: Na pierwszym miejscu w pracy stawiam dopełniający się bez reszty regularny podział płaszczyzny. We wszystkich rysunkach z ostatnich kilku lat pokrywam ją całkowicie przystającymi figurami, nie pozostawiając ani kawałka wolnej przestrzeni; moje rysunki nie maja końca i powtarzają się na nich bez przerwy te same elementy.

Mistrzami sztuki wypełniania płaszczyzny powtarzającym się motywem byli Maurowie, którzy w motywach dekoracyjnych często wykorzystywali mozaiki z figur geometrycznych. Fascynacja Eschera tym tematem była efektem podróży do Hiszpanii w 1922 roku i zauroczenia pięknem widzianych w pałacu Alhambra w Granadzie geometrycznych wzorów islamskich. Zainspirowany arabskimi ornamentami holenderski twórca zapełniał odtąd płaszczyznę rybami, ptakami, gadami, pajacami i innymi postaciami o przedziwnych kształtach, a do projektowania tych figur wykorzystywał przekształcenia geometryczne - symetrie, translacje i obroty. Uzyskiwał w ten sposób zaskakujące wzory, noszące dziś nazwę parkietaży escherowskich. Ich strukturę można opisać i sklasyfikować, stosując dwuwymiarowe grupy symetrii (tzw. grupy tapetowe).

Escherowskie pokrycia płaszczyzny urzekają magią ornamentu, ale są tylko pochodnymi regularnych pokryć płaszczyzny jednakowymi wielokątami. Aby ułatwić wam wyobrażenie sobie kolejnych etapów tworzenia takich obrazów, a zwłaszcza zaprojektowania tworzącego je kafelka, na zamieszczonych poniżej rysunkach mozaik Eschera zaznaczono tzw. obszar fundamentalny, który przekształcony został za pomocą podstawowych izometrii płaszczyzny: przesunięcia, obrotu, symetrii osiowej, symetrii środkowej i symetrii z poślizgiem w motyw pozwalający na wygenerowanie całego pokrycia. Można dokładnie przeanalizować, w jaki sposób odkształcono boki poszczególnych wielokątów i jak wybór obszaru fundamentalnego wpłynął na ostateczny efekt symetrii.

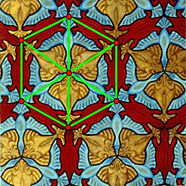
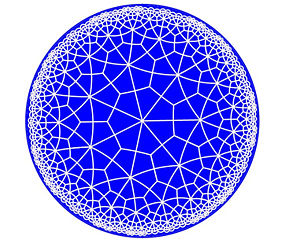
Od spotkania na Międzynarodowym Kongresie Matematycznym w 1954 roku Escher korespondował ze znanym kanadyjskim geometrą H.S.M. Coxeterem. Ogromne wrażenie wywarł bowiem na nim rysunek z jednej z prac Coxetera przedstawiający pokrycie płaszczyzny trójkątami hiperbolicznymi, którego szkic zaczerpnięty z pracy Douglasa Dunhmana "Hyperbolic art and poster pattern" przedstawiamy obok.

Od tego czasu szczególnie zainteresowały Eschera parkietaże koła z ornamentem malejącym w miarę zbliżania się do brzegu figury. Na podstawie otrzymanego od Coxetera rysunku zrekonstruował siatkę łuków, a następnie wykorzystał ją do utworzenia interesujących parkietaży płaszczyzny z geometrią nieeuklidesową. Grafiki opatrzone tytułem "Granice koła" (z lat 1958-1960) to artystyczna wizja modelu Poincarego płaszczyzny z geometrią Łobaczewskiego. Ukazanie nieskończoności zawartej w skończonym obszarze doskonale oddaje ideę geometrii hiperbolicznej.

"Granice koła I" – drzeworyt langowy, 1958	"Granice koła II" - drzeworyt langowy, 1959
"Granice koła III" – drzeworyt langowy, 1954	"Granice koła IV" albo "Niebo i piekło" – drzeworyt langowy, 1960

Grafiki te stały się tematem poważnych analiz matematycznych oraz inspirowały artystów do tworzenia kolejnych hiperbolicznych obrazów. Sam Coxeter zachwycony zawartą w nich matematyczną głębią poddał je szczegółowej analizie i potwierdził niezwykłą matematyczną precyzję, z jaką zostały wykonane, dokładnie wpisując się w siatkę łuków triangulacji dysku Poincarego. "Granice koła" I, II i IV bazują na łukach ortogonalnych do brzegu. Natomiast "Granice koła" III także wykorzystuje łuki okręgów, jednak tym razem nie są one prostopadłe i nie tworzą parkietażu hiperbolicznego. Escher wykorzystał tu ekwidystanty, czyli linie równoodległe od łuków triangulacji ortogonalnej.

Jednym z najbardziej intrygujących dzieł Eschera jest litografia "Galeria grafiki" (1956). Patrząc na nią, zadajemy sobie pytanie, czy można być jednocześnie wewnątrz i na zewnątrz obrazu. Wyraźnie widzimy tutaj powiększenie postępujące wokół pozornie pustego środka zgodnie z ruchem wskazówek zegara. Młodzieniec, spoglądając na obraz w galerii, widzi morze, statek, powiększone miasto, a w nim... galerię grafiki, w której odnajduje siebie wpatrzonego w morze... Wyjątkową tajemnicą, a jednocześnie inspiracją dla badaczy twórczości Eschera okazała się pozostawiona na środku obrazu pozornie biała plama.

Jesteśmy tylko chwilowym produktem ewolucji, jak pisał Teihard de Chardin. Jeśli miał rację, ewolucja skończy się w tajemniczym "punkcie Omega" po milionach lat. Skoro tak, to dlaczego nie? - pisał Escher w liście do syna George’a w 1962 roku. 

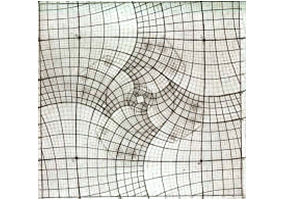
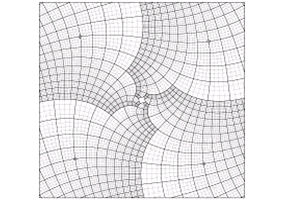
Obraz ten ma niezwykle interesującą strukturę matematyczną, kojarzącą się ze specjalnym rodzajem obrazu rekurencyjnego, tzw. efektem Drosta. Do opisu występujących na takim obrazie zniekształceń wykorzystuje się wykładnicze funkcje zespolone. Matematyczne symulacje i badania nad grafiką Eschera przedstawili w pracy "The mathematical structure of Escher’s 'Print gallery'" B.de Smit i H.W. Lenstr Jr. Na poniższych rysunkach widzimy siatkę obrazu ze szkiców Eschera oraz podobną bardzo podobną siatkę uzyskaną przez Lenstra za pomocą funkcji zespolonych.

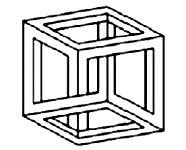
Escher zainspirowany przez prace brytyjskiego fizyka i matematyka Rogera Penrose’a zanteresował się także złudzeniami optycznymi i architekturą niemożliwą. W wielu jego grafikach można odnaleźć podstawowe figury niemożliwe, np. niemożliwy trójkąt Penrose’a, niemożliwy sześcian Neckera czy schody prowadzące donikąd.

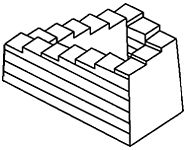Trójkąt Penrose'a	Sześcian Neckera	Schody Penrose'a
"Wodospad" – litografia, 1961	"W górę i w dół" – litografia, 1960	"Belweder" - fragment

Matematyka i sztuka to tylko pozornie odległe obszary. Przeciętny odbiorca sztuki Eschera często nie uświadamia sobie, że obcuje z matematyką. Jednak współczesne techniki multimedialne otwierają przed wszystkimi drogę do wyjątkowej działalności artystycznej. Pojawiło się pojęcie matematycznej sztuki komputerowej, w szczególności sztuki algorytmicznej, czyli dzieła wygenerowane za pomocą matematycznych algorytmów. I one równie głęboko pobudzają ludzką wyobraźnię i wrażliwość na piękno. Wiele przykładów takiej twórczości można znaleźć w internecie.
Escher był prekursorem takich działań. Pokazał, że nawet proste techniki teselacji, bez pogłębionej wiedzy matematycznej, mogą prowadzić do nietuzinkowego artystycznego efektu. Wykorzystując możliwości współczesnych programów komputerowych, możemy założyć własną pracownię artystyczną i tworzyć własne fantastyczne wizje. Nie potrzeba do tego profesjonalnych programów do grafiki komputerowej. Popularne programy do geometrii dynamicznej (np. GeoGebra, Cabri, Geomatry Skatchpad) pozwalają na pierwsze eksperymenty ze sztuką matematyczną. Można też wykorzystać freewerowy program Tess do projektowania teselacji.

Sztuka matematyczna może być dostępna dla każdego, a kluczem do jej poznania może być twórczość M.C. Eschera. Zachęcamy do jej zgłębiania i do własnych eksperymentów.

Poniższe mozaiki hiperboliczne powstały w programie Geometry Sketchpad 5.01 a modele teselacji za pomocą programu Tess.

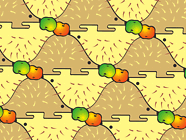
O rozmaitych puzzlach i łamigłówkach wykorzystujących grafiki Eschera przeczytasz na Portalu tutaj.

• http://www.mcescher.com - oficjalna strona fundacji Eschera
• www.escherinhetpaleis.nl - strona Muzeum Eschera w Hadze
• http://www.worldofescher.com - sklep internetowy i konkurs na teselację
• http://www.cs.technion.ac.il/~gershon/EscherForReal - Escher for Real
• http://www.britton.disted.camosun.bc.ca/jbescher.htm - Escher in the classroom
• http://library.thinkquest.org/16661/escher.html - Totally Tessellated
• http://www.math.nus.edu.sg/aslaksen/gem-projects/maa/0203-2-03-Escher/ma... -  Mathematics behind the art of Escher
• http://mathaware.org/mam/03/essay1.html - D. Dunham, Hyperbolic Art and the Poster Pattern
• http://www.d.umn.edu/~ddunham/dunham.am.pdf - D. Dunham, The Family of "Circle Limit III" Escher Patterns
• http://www.msri.org/people/members/sara/articles/siamescher.pdf - Sara Robinson, M.C. Escher. More Mathematics than Meets the Eye
• http://www.ams.org/notices/200304/fea-escher.pdf - Artful Mathematics: The Heritage of M.C. Escher, Celebrating Mathematics Awareness Month
• http://escherdroste.math.leidenuniv.nl - Escher and the Droste Effect
• http://www.josleys.com/article_show.php?id=82 - Jos Leys, An logarithmic image transformation
• M.C. Escher, The Graphics Work, Taschen
• Magia M.C. Eschera, Taschen

• http://gallery.wolfram.com
• http://www.kfunigraz.ac.at/imawww/vqm/pages/colorgallery/index.html
• http://virtualmathmuseum.org/mathart/MathematicalArt.html
• http://www.tessellations.org