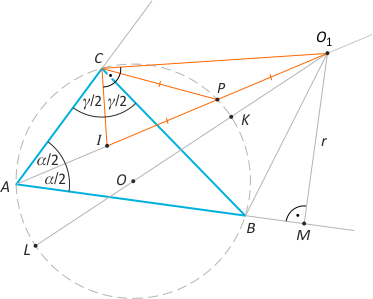
Zad. 1. W trójkącie prostokątnym ABC poprowadzono dwusieczną CD kąta prostego. Wiedząc, że |AD|=m i |DB|=n, oblicz wysokość opuszczoną na przeciwprostokątną.
Zad. 2. Na trójkącie ABC opisano okrąg i poprowadzono do niego styczną w punkcie A, która przecina prostą BC w punkcie D. Oblicz długość odcinków AD i DB, wiedząc, że |BC|=a, |AC|=b i |AB|=c.
Zad. 3. Na trójkącie ABC opisano okrąg s. Wykaż, że okręgi symetryczne do s względem prostych AB, BC i AC przecinają się w ortocentrum trójkąta (czyli w punkcie przecięcia prostych zawierających wysokości trójkąta).
Zad. 4. (wolna amerykanka) Niech O i R oznaczają odpowiednio środek i promień okręgu opisanego na trójkącie ABC, a O1 i r - środek i promień dowolnego okręgu dopisanego do tego trójkąta. Wykaż, że |OO1|2 = R2 + 2rR.
Za zadania 1 - 3 punkty otrzymali:
30 - Jacek Baginski (nauczyciel matematyki, I LO Kraków), Ela Grzechnik
(emerytowany nauczyciel, Radom)i Mikołaj Popek (student UAM)
28 - Dominik Bysiewicz (student UJ), Tadeusz Porzucek (emerytowany nauczyciel,
Gostyń) i Janusz Wieczorek (emerytowany nauczyciel, Sandomierz)
20 - Joanna Koścień (nauczyciel SP 14, Piekary Śląskie)
18 - Mateusz Bielówka (I LO Kraków)
16 - Filip Derejski (I LO Kraków)
Za zadanie 4 punkty otrzymali:
10 - Jacek Bagiński, Dominik Bysiewicz, Mikołaj Popek, Tadeusz Porzucek i
Janusz Wieczorek
Gratulacje.
Zad. 1. Skorzystamy z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta. Oznaczmy długości boków jak na rysunku. Rozwiązując układ równań a2m2 + a2n2 = (m+n)2 oraz a2mn/2 = h(m+n)/2, otrzymujemy h = mn(m+n)/(m2+n2).
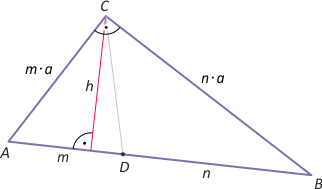
Zad. 2. Wprowadźmy oznaczenia jak na rysunkach. Rozważmy dwa przypadki: b<c i b>c, bo gdy b i c są równe, styczna i prosta BC nie przecinają się. W obu przypadkach skorzystamy z twierdzenia o stycznej i siecznej okręgu oraz z podobieństwa trójkątów ACD i ABD. Rozwiązując układy równań:
(I) x2 = y(y+a) oraz x/b = (a+y)/c
(II) x2 = y(y+a) oraz (4) x/b = y/c,
otrzymujemy wyniki:
(I) y = ab2/(c2–b2) i x = abc/(c2–b2)
(II) y = ac2/(b2–c2) i x = abc/(b2–c2).
Ostatecznie |AD| = abc/|c2–b2| oraz |BD| = ac2/|c2–b2|.
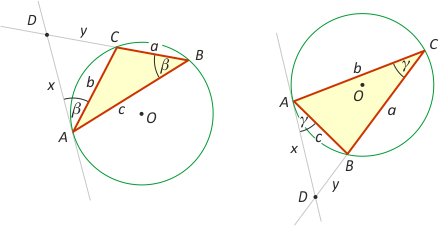
Zad. 3. Skorzystamy z faktu, że odległość środka okręgu opisanego od boku trójkąta jest dwa razy mniejsza niż odległość przeciwległego wierzchołka od ortocentrum (patrz zadanie 3, maj 2015). Niech O1, O2 i O3 to obrazy środka O w symetrii względem odpowiednich boków. Zauważmy, że czworokąty AOO1H, BHO2O i CHO3O, są równoległobokami. Ich wspólnym punktem jest ortocentrum H (tzn. punkt przecięcia wysokości trójkąta). Zachodzi |OC| = |O1C| = |OB| = |O1B| = |OA| = |O1H| = R. Oznacza to, że H należy do okręgu symetrycznego do opisanego względem boku BC. Pozostałe przypadki rozważamy analogicznie. W przypadku trójkąta prostokątnego jeden z równoległoboków redukuje się do odcinka.
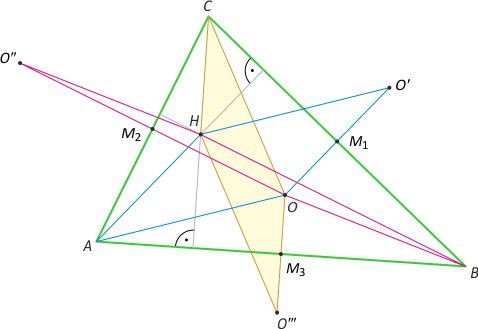
Zad. 4. (wolna amerykanka) Z twierdzenia o siecznych okręgu mamy |O1K|·|O1L| = |O1P|·|O1A| = (|O1O|–R)·(|O1O|+R) = |O1O|2–R2. W trójkącie AMO1 mamy |O1A| = r/sin(α/2). Z kolei w trójkącie CIO1 mamy (*) |O1P| = |CP| (dowód poniżej), a z twierdzenia sinusów w trójkącie APC mamy |CP| = 2Rsin(α/2). Ostatecznie otrzymujemy |OO1|2 = 2Rsin(α/2)·r/sin(α/2)+R2 = 2Rr+R2.
Dowód (*). Kąt ICO1 jest prosty, bo CI i CO1 są dwusiecznymi kątów przyległych. Łatwo zauważyć, że |<CIP| = |∡ICP| = α/2 + γ/2, a |<PCO1| = |∡PO1C| = 90°–(α+γ)/2. Oznacza to, że trójkąty IPC oraz PO1C są równoramienne i |IP| = |CP| = |PO1|.