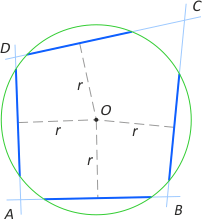
Zad. 1. Wykaż, że jeśli przy przecięciu okręgu z brzegiem czworokąta wypukłego powstają cztery równej długości cięciwy, to sumy długości przeciwległych boków czworokąta są równe.
Zad. 2. Z punktu A poprowadzono styczne AM i AN do okręgu (gdzie M i N są punktami styczności) oraz sieczną przecinającą ten okrąg w punktach P i Q. Niech L będzie środkiem odcinka PQ. Wykaż, że kąty MLA i NLA mają równe miary.
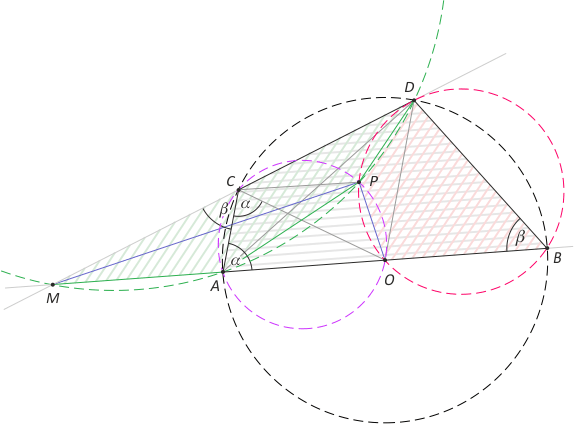
Zad. 3. Przez punkt M leżący na zewnątrz okręgu poprowadzono dwie sieczne tego okręgu. Jedna z nich przechodzi przez środek O okręgu i przecina go w punktach A i B. Druga przecina okrąg w punktach C i D. Okręgi opisane na trójkątach AOC i BOD przecinają się w punkcie P. Wykaż, że kąt MPO jest prosty.
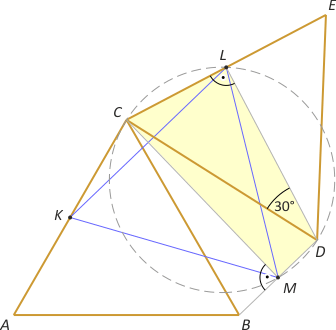
Zad. 4. (wolna amerykanka) Trójkąty równoboczne ABC i CDE o boku długości 1 mają jeden punkt wspólny C, a kąt BCD ma miarę mniejszą niż 60°. Niech K będzie środkiem odcinka AC, L - środkiem odcinka CE, a M - środkiem odcinka BD. Pole trójkąta KLM wynosi (√3)/5. Oblicz długość BD.
Za zadania 1 - 3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student UJ) i Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 20 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Elżbieta Grzechnik (emerytowany nauczyciel, Radom), Mikołaj Popek (student UAM) oraz Janusz Wieczorek (emerytowany nauczyciel, Sandomierz),
- 10 - Mateusz Bielówka (I LO Kraków) i Joanna Koścień (nauczyciel SP 14, Piekary Śląskie).
Za zadanie 4 po 10 pkt. otrzymali: Jacek Bagiński, Dominik Bysiewicz, Mikołaj Popek, Tadeusz Porzucek i Janusz Wieczorek. Gratulujemy!
Zad. 1. Zauważmy, że środek okręgu O leży w tej samej odległości od każdej z cięciw. Jest zatem jednocześnie środkiem okręgu wpisanego w czworokąt, a stąd wynika teza.
Zad. 2. Zauważmy, że punkty A, M, O, L i N leżą na jednym okręgu o średnicy AO. Wówczas podane w treści zadania kąty są przystające, bo są wpisane w okrąg i oparte na cięciwach równej długości (|AM|=|AN|).

Zad. 3. Oznaczmy |∡MCA|=β i |∡CAO|=α. Wówczas |∡ABD|=β, bo czworokąt ABDC jest wpisany w okrąg, a |∡ACO|=α, bo trójkąt AOC jest równoramienny. Dalej czworokąty AOPC i OBDP też są wpisane w okrąg, stąd |∡APO|=α oraz |∡DPO|=180°–β. Otrzymujemy zatem |∡DPA| = 360°–|∡DPO|–|∡APO| = 180°+β–α. Z drugiej strony |∡DMA| = |∡CMA| = α–β. Zauważmy
teraz, że |∡DPA|+|∡DMA| = 180°, co oznacza, że punkty M, A, P i D są współokręgowe. Wynika stąd równość miar kątów wpisanych |∡MDA| = |∡MPA| = |∡CDA| = |∡CDB|–90° = (180°-α) – 90° = 90°–α. Miarę kąta CDB można obliczyć, korzystając z faktu, że czworokąt ABDC jest wpisany w okrąg. Ostatecznie |∡MPO| = |∡MPA|+|∡APO| = 90°.
Zad. 4. (wolna amerykanka) Zauważmy, że DL i CM są wysokościami w trójkątach równoramiennych, stąd |∡CLD| = |∡CMD| = 90°. Oznacza to, że na czworokącie CMDL można opisać okrąg, zatem |∡CML|=|∡CDL|= 30°. Analogicznie (symetria względem prostej CM) |∡CMK| = 30°, skąd |∡KML| = 60° i trójkąt KML jest równoboczny. Korzystając z podanego pola trójkąta KLM, łatwo obliczyć, że |KL| = (2√5)/5. Z twierdzenia kosinusów w trójkącie KLC mamy |KL|2 + 1/4 + 1/4 – (1/2)·cos(∡KCL), skąd otrzymujemy cos(∡KCL) = -(3/5). Rozważmy teraz trójkąt BDC. Mamy |∡BCD| = |∡KCL|–120°. Stosując twierdzenie kosinusów do trójkąta BDC, mamy |BD|2 = |BC|2 + |DC|2 – 2 |BC|·|DC|·cos(∡BCD) = (7–4√3)/5, skąd |BD| = (2–√3)/√5.