Zad. 1. Przy okrągłym stole ma usiąść 2023 matematyków. Każdy z nich ma dokładnie 1000 wrogów. Czy można tak usadzić matematyków przy stole, by żaden nie siedział bezpośrednio obok swojego wroga?
Zad. 2. W sześcianie o wymiarach 8×8×8 rozważmy trzy ściany o wspólnym wierzchołku. Ilu co najmniej pasków papieru o wymiarach 3×1 należy użyć, by okleić powierzchnię tych ścian? Oklejamy wyłącznie zewnętrzną stronę powierzchni.
Zad. 3. Dla jakich liczb pierwszych p liczby p2+4 oraz p2+6 są pierwsze?
W tym miesiącu nie przyznano punktów za rozwiązania zadań.
Zad. 1. Usadźmy matematyków losowo. Jeżeli żaden nie siedzi obok swojego wroga, otrzymaliśmy żądane ustawienie. W przeciwnym wypadku ponumerujmy matematyków kolejno (2. siedzi na lewo od 1. itd.) i załóżmy, że pierwszy i drugi są wrogami. Rozważmy 1023 przyjaciół pierwszego matematyka. Niektórzy ich sąsiedzi z lewej strony muszą być przyjaciółmi drugiego matematyka (gdyż maksymalnie tysiąc z nich jest jego wrogami). Niech więc n będzie najmniejszą taką liczbą, że n-ty matematyk jest przyjacielem pierwszego, a (n+1)-szy jest przyjacielem drugiego. Odwracając kolejność wszystkich osób siedzących na miejscach od drugiego do n-tego włącznie:
- usunęliśmy wrogość pomiędzy miejscami 1 a 2,
- nie zmieniliśmy liczby wrogości pomiędzy matematykami zmieniającymi miejsca,
- nie wprowadziliśmy wrogości pomiędzy miejscami n a n+1.
Taka operacja zmniejsza liczbę wrogości na sąsiednich miejscach. Ponieważ zbiór liczb naturalnych jest ograniczony z dołu, tej operacji nie można wykonywać w nieskończoność - w którymś momencie nie będzie się dało jej wykonać. Jest to równoważne temu, że każdy matematyk siedzi między dwojgiem swoich przyjaciół.
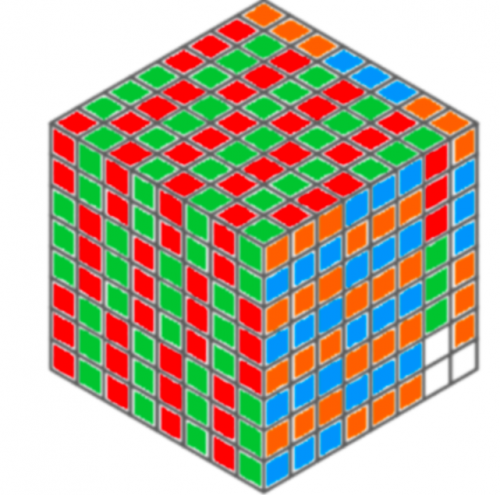
Zad. 2. Minimalna liczba pasków wynosi 65. Wiadomo, że jeśli pasków będzie mniej niż 64, nie wystarczy ich do pokrycia wszystkich pól. Pokażemy, że 64 też nie wystarczy. Pokolorujmy sześcian w sposób pokazany na poniższym rysunku.

Widzimy, że liczba białych pól jest nieparzysta, a każdy pasek zakrywa 0 lub 2 białe pola. Jednocześnie paski nie mogą się pokrywać, gdyż nie wystarczyłoby ich do zakrycia całego sześcianu. Natomiast 65 pasków wystarczy. Na poniższym rysunku użyliśmy ich 63, zostały więc jeszcze dwa do pokrycia pozostałych białych pól.
Zad. 3. Każdy kwadrat daje resztę z dzielenia przez 5 równą -1, 0 lub 1. Gdyby p2 dawało resztę -1, to p2+6 byłaby podzielna przez 5. Gdyby zaś p2 dawało resztę 1, to p2+4 byłaby wielokrotnością 5, ale liczby te mają być pierwsze, czyli musiałyby być równe 5. Implikowałoby to odpowiednio p2=1 lub p2=-1, co stanowi sprzeczność z pierwszością. Jedyny pozostały przypadek to p=5. Łatwo sprawdzić, że wtedy warunki zadania są spełnione.







