Zad. 1. Poniżej pokazany jest przykład rachunkowy z pewnego podręcznika dla SP i klucz odpowiedzi. Skomentuj problem.
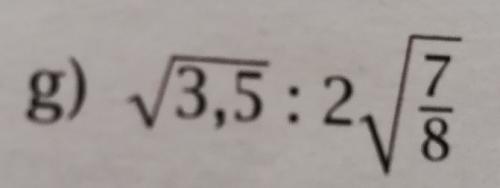
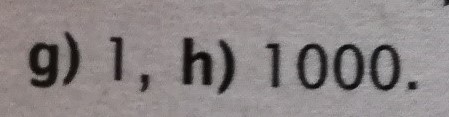
Zad. 2. Uczeń LO twierdzi, że po złożeniu funkcji z funkcją do niej odwrotną zawsze w wyniku wychodzi identyczność. Czy ma rację?
Zad. 3. Co to jest sprzężenie liczby? Odpowiedz na poziomie szkolnym.
W tym miesiącu punkty otrzymali:
- 3 - Karolina Kochanowska - entuzjastka nauczania z Lublina,
- 2,75 - Adam Wrzesiński - terapeuta z Bielska-Białej,
- 2 - Tomasz Tomiczek - nauczyciel z Lipowej,
Zad. 1. Problem wynika z różnej interpretacji kolejności działań i zapisu mnożenia z opuszczoną kropką. Zapis 2√a oznacza mnożenie 2 · √a. W przypadku mnożenia i dzielenia (które są równoprawne w sensie kolejności działań) wykonujemy je kolejno od lewej do prawej. Zatem w podanym działaniu należy wykonać dzielenie liczby √3,5 przez 2, a następnie mnożenie przez
7/8. Wówczas otrzymamy wynik 0,875 (niezgodny z kluczem odpowiedzi) i taki wynik pokaże każdy kalkulator. Jednak istnieje konwencja, zgodnie z którą opuszczenie znaku mnożenia traktowane jest jako dostawienie nawiasu, np. 2a należy rozumieć jako (2·a). Większość wszak uzna, że wykresem funkcji sin 2x jest sinusoida, a nie prosta o współczynniku kierunkowym sin2. W tej konwencji napis z zadania należy rozumieć jako √3,5 : [tex](2 \cdot \sqrt \frac{7}{8}) [/tex] i wówczas wynikiem jest 1, bo jako pierwsze wykonujemy działanie w nawiasie, które ma bezwzględne pierwszeństwo. Umowa dotycząca kolejności działań jest podawana oficjalnie w podręcznikach szkolnych. Umowa dotycząca opuszczania znaku mnożenia jest stosowana powszechnie, ale ani nie jest explicite w podręcznikach formułowana, ani nie jest oczywista. Reguła jest taka, że zapisując dzielenie bardziej skomplikowanych wyrażeń arytmetycznych za pomocą znaków ':' lub '/' należy licznik i mianownik wstawić w nawiasy. Lepiej nadużyć nawiasów niż doprowadzić do sytuacji błędnej interpretacji zapisu działania.
Zad. 2. Uczeń ma rację, o ile rozumie, że różnych funkcji identycznościowych jest nieskończenie wiele, bo dziedziną takiej funkcji nie muszą być liczy rzeczywiste. Funkcję identycznościową oznaczamy nawet jako idS, gdzie S jest dziedziną tej funkcji. Zatem wykresem złożenia funkcji z funkcją do niej odwrotną jest zawsze funkcja o wzorze analitycznym y=x, ale nie zawsze jest to prosta y=x (czyli wykres idR), może to być jedynie fragment tej prostej. Rozważmy następujące przykłady funkcji f i ich złożeń z funkcjami do nich odwrotnymi (złożenie f z f-1 zaznaczono linią pogrubioną).
a) f(x) = 2x, wtedy f -1(x) = 0,5x , a f -1 ° f (x) = x = idR
b) f(x) = 1/x, wtedy f -1(x) = 1/x , a f -1 ° f (x) = x = idR\{0}
c) f(x) = √x, wtedy f -1(x) = x2, a f -1 ° f (x) = x = idR+
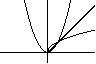
d) f(x) = ex, wtedy f -1(x) = lnx, a f -1 ° f (x) = x = idR
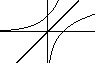
d') f(x) = lnx, wtedy f -1(x) = ex, a f -1 ° f (x) = x = idR+
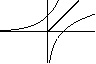
e) f(x) = arcsinx, wtedy f -1(x) = sinx, a f -1 ° f (x) = x = id[0, 1]

W niektórych rozwiązanich podano, że uczeń nie ma racji, bo wykresem złozenia funkcji odwrotnych może też być wykres wartości bezwzględnej x, a nawet funkcja piłokształtna, które nie są wykresami identyczności na żadnym zbiorze. W tych wypadkach chodziło o następujące złożenia:
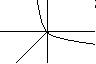
c') f(x) = x2, wtedy f -1(x) = √x, a f -1 ° f (x) = |x| ≠ idR
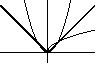
e') f(x) = sinx, wtedy f -1(x) = arcsinx, a f -1 ° f (x) ≠ idR
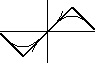
Oczywiście te złożenia istnieją i naprawdę ich wykresy mają taki kształt, ale... nie są to złożenia funkcji odwrotnych. Z definicji funkcje y=x2 oraz y=sinx określone na R nie mają funkcji odwrotnych, bo nie są różnowartościowe. Można wyznaczyć do nich funkcje odwrotne tylko wtedy, gdy ograniczymy dziedziny tych funkcji do zbiorów, na których są one różnowartościowe. Wówczas wyznaczone do nich funkcje odwrotne (niekoniecznie te podane wyżej) po złożeniu dadzą identyczność na tych zbiorach. Na przykład dla funkcji f(x) = x2 określonej na zbiorze (-∞, 0) funkcją odwrotną jest f -1(x) = -√x, a f -1 ° f (x) = idR-.
Można też podejść do problemu teoriomnogościowo i potraktować funkcje y=x2 lub y=sinx jako relacje, czyli podzbiory iloczynu kartezjańskiego R×R, tzn. zbiory {(x, y): y=x2} oraz {(x, y): y=sinx}. Wtedy można wyznaczyć do nich relacje odwrotne, ale nie będą one funkcjami (będą wielowartościowe).
Zad. 3. Dla liczby postaci a +*b, gdzie a i b należą do zbioru liczbowego X, a * jest jednoargumentowym działaniem wykonywanym na liczbach ze zbioru X, którego wynik może nie należeć do X, ale jego kwadrat już należy, liczbą sprzężoną jest liczba a –*b. Wówczas suma i iloczyn liczb sprzężonych dają liczby ze zbioru X. Sprzężenie jest inwolucją, tzn. zastosowane dwukrotnie do dowolnej liczby daje wyjściową liczbę.
Przykłady:
a) X = Q, * to pierwiastkowanie, liczby sprzężone to a+√b i a–√b
Własności:
- Mnożenie przez liczbę sprzężoną stosuje się np. w celu usunięcia niewymierności z mianownika ułamka.
- Jeżeli jakaś liczba niewymierna jest pierwiastkiem wielomianu o współczynnikach wymiernych, to liczba do niej sprzężna także.
b) X = R, * mnożenie przez √(-1) = i, liczby sprzężone to a+bi i a–bi
Własności:
- Mnożenie przez liczbę sprzężoną stosuje się np. w celu usunięcia urojoności z mianownika ułamka.
- Jeżeli jakaś liczba zespolona jest pierwiastkiem wielomianu o współczynnikach rzeczywistych, to liczba do niej sprzężona także.







