Zadanie 1. W trójkąt ABC wpisano trzy półokręgi o promieniach Ra, Rb i Rc, których średnice zawierają się w odpowiednich bokach. Wykaż, że suma odwrotności długości tych promieni jest dwa razy większa od odwrotności długości promienia r okręgu wpisanego w ten trójkąt .
Zadanie 2. W trójkąt równoramienny wpisano kwadrat o polu 1 (bok kwadratu leży na podstawie). Oblicz pole trójkąta, wiedząc, że środki ciężkości obu figur pokrywają się.
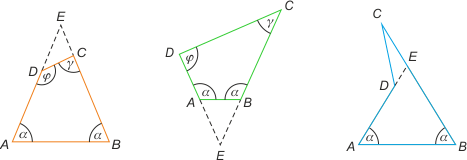
Zadanie 3. W czworokącie ABCD kąty A i B są przystające, a kąt D jest większy niż kąt C. Wykaż, że bok AD jest krótszy od BC.
Maksymalną liczbę 30 punktów w tym miesiącu zdobył jedynie pan Włodzimierz Bąk (nauczyciel, I LO Opole). 28 punktów zdobyli: Jacek Bagiński (nauczyciel, I LO Kraków), Krzysztof Sobków (nauczyciel, II LO Opole) oraz Arkadiusz Wróbel (student, Brwinów). Tak też wygląda czołówka Ligi po trzech miesiącach. Gratulujemy.
Życzymy wszystkim udanego Nowego Roku i wiele przyjemności przy rozwiązywaniu kolejnych zadań.
 Zadanie 1
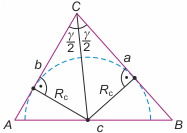
Zadanie 1
Wykorzystamy pomocniczo pole trójkąta ABC (wyrazimy je dwoma sposobami). Rozważmy półkole o środku na boku AB i promieniu Rc. Wówczas PABC = 1/2bRc + 1/2aRc = 1/2Rc(a+b) = pr, gdzie r to promień okręgu wpisanego w trójkąt, a p to połowa obwodu trójkąta. Stąd 1/Rc = (a+b)/2pr. Analogicznie 1/Ra = (b+c)/2pr oraz 1/Rb = (a+c)/2pr. Dodając te wyrażenia stronami, otrzymujemy tezę.
 Zadanie 2
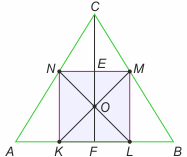
Zadanie 2
Zauważmy, że bok kwadratu wynosi 1 i OF = 1/2, zatem z własności środka ciężkości trójkąta mamy CO = 1. Dalej CE = 1/2 = NE, co znaczy, że ∡CNE = 45° = ∡CAB. Zatem trójkąt ABC jest prostokątny i jego pole wynosi 9/4.
Zadanie 3
Rozważymy różne przypadki. Przedłużmy boki AD i BC do przecięcia się w punkcie E. Otrzymamy wówczas trójkąty równoramienne ABE. Dalej wykorzystamy odpowiednio fakt, że naprzeciw większego kąta w trójkącie leży dłuższy bok (np. na rys. a w trójkącie DEC kąt C jest większy niż kąt D, stąd ED jest dłuższy niż EC). Odejmując od równych ramion AE i BE odcinki EC i ED, otrzymujemy tezę. W pozostałych przypadkach rozumowanie jest analogicznie. Przypadek α = 90° jest oczywisty.