| więcej informacji o tekście: |
Właściwie cała szkolna (i nie tylko) geometria opiera się na własnościach trójkątów podobnych i twierdzeniu Talesa. Choć są to elementarne fakty znane każdemu gimnazjaliście, korzysta się z nich także w najbardziej zaawansowanych problemach syntetycznej geometrii i w wielu zadaniach olimpijskich. Można zaryzykować stwierdzenie, że sukces nauczania geometrii opiera się na wyrobieniu pewnej biegłości w dostrzeganiu podobieństwa trójkątów i proporcji geometrycznych.
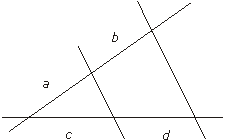
Jeśli ramiona kąta przetniemy prostymi równoległymi, powstanie wiele par proporcjonalnych odcinków. Niektóre z tych proporcji wynikają z własności trójkątów podobnych (które?), a jedna szczególna, została nazwana twierdzeniem Talesa.
O błędnych sformułowaniach tego twierdzenia można przeczytać tutaj.
Niezwykle elegancki, jednolinijkowy dowód twierdzenia Talesa został zamieszczony w Elementach Euklidesa. Korzysta jedynie z faktu, że pole trójkąta jest proporcjonalne do podstawy i wysokości opuszczonej na tę podstawę.
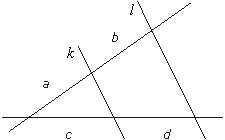
Jeśli ramiona kąta przetniemy prostymi k i l, które utworzą na tych ramionach odcinki proporcjonalne a:b = c:d, to proste k i l są równoległe.
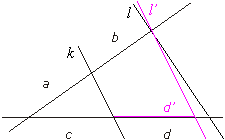
Ten fakt można bardzo łatwo udowodnić z... twierdzenia Talesa. Załóżmy bowiem, że proste k i l nie są równoległe. Wtedy możemy dorysować prostą l' równoległą do k, jak na rysunku, i na podstawie prostego twierdzenia Talesa otrzymamy proporcję a:b = c:d', co przeczy równości a:b = c:d, bo d jest różne od d'.
Jak zwykle w zadaniach praktycznych trzeba przyjąć dodatkowe założenia, które idealizują rzeczywistość, ale jednocześnie umożliwiają zastosowanie w rozwiązaniach metod matematycznych, bo przecież matematyka działa tylko na abstrakcyjnych modelach, nie rzeczywistych obiektach.
Tradycyjnie do zadań nie robimy rysunków. Bardzo ważne jest, by uczeń sam wyobraził sobie opisywaną sytuację i wykonał rysunek. Analiza jego poprawności jest jednym z najważniejszych etapów rozwiązania zadania.
Sytuacje płaskie
1. Park pałacowy miał kształt trapezu równoramiennego, o krótszej podstawie 8 jardów, długości ramienia 13 jardów i wysokości 12 jardów. Królewski ogrodnik postanowił zwiększyć jego powierzchnię dodając obszar ograniczony przedłużeniami ramion trapezu aż do punktu ich przecięcia. Jaki obwód i jakie pole powierzchni będzie miał powiększony park?
2. Ogród jordanowski ma kształt równoległoboku o krótszej przekątnej 480 m. Wokół niego wykopano kanał o szerokości 4 m, po którym można pływać kajakami. Z kolei wzdłuż zewnętrznego brzegu kanału poprowadzono alejkę, a na środku jej dwóch sąsiednich boków postawiono budkę z lodami i drugą z watą cukrową. Przed każdą z nich przerzucono mostek nad kanałem prowadzacy na teren ogrodu. Jak długa droga dzieli budki z łakociami, jeśli chcemy przejść przez dwa mostki i na skróty przez ogród?
3. Ulice Wschodnia i Zachodnia biegną równolegle i równoleżnikowo. Obszar między nimi wypełnia skwer z zielenią. Na wschodnim krańcu Wschodniej jest kościół, a na zachodnim - bank. Na wschodnim krańcu Zachodniej jest sklep spożywczy, a na zachodnim - szkoła. Z kościoła do szkoły i ze sklepu do banku mieszkańcy wydeptali przez skwer ścieżki na skróty, które potem wyłożono płytami chodnikowymi. W miejscu przecięcia się tych alejek postawiono pomnik Geometry. Jaka jest jego odległość od szkoły, jeśli:
a) od pomnika do kościoła jest 900 m, do sklepu 1 km, a bank od sklepu dzieli 2,2 km.
b) odległość sklep-szkoła wynosi 400 m, bank-kościół 600 m, a kościół dzieli od szkoły 1,5 km.
4. Torcik wedlowski (dawniej 22 Lipca) w kształcie trójkąta równoramiennego ma 8 cm w podstawie i wysokość 6 cm. Mama przekroiła go jednym cięciem noża równolegle do podstawy, tak że linia cięcia ma 4,8 cm. Część trójkątną dostał Jacek, a czworokątną Placek. Czy ten podział był sprawiedliwy? Jaką część torcika dostał każdy z braci? W jakiej odległości od wierzchołka powinno wypaść cięcie, aby podział był sprawiedliwy?
5. Dany jest trójkąt ABC. Jak skonstruować za pomocą cyrkla i linijki trójkąt o polu dwa razy większym i o bokach równoległych do boków trójkąta ABC?
Proste sytuacje przestrzenne
1. Mam 160 cm wzrostu, a mój cień ma w tej chwili 180 cm długości. Drzewo obok mnie rzuca cień o długości 3,6 m. Jaka jest wysokość tego drzewa?
2. Janek świeci latarką na biały ekran z odległości 80 cm, uzyskując koło o średnicy 1 m. Co powinien zrobić, aby średnica koła na ekranie wynosiła 1,5 m?
3. Ania postanowiła zmierzyć szerokość rzeki w miejscu, gdzie w pobliżu nie było mostu, za to na przeciwległym brzegu, tuż nad wodą rosło drzewo. Stanęła twarzą w kierunku drzewa, mając je na linii prostopadłej do osi rzeki, w pewnej odległości od brzegu, potem odwróciła się w prawo, przemaszerowała 15 m i odwróciła znowu twarzą w kierunku drzewa. Następnie zaczęła iść w tym kierunku aż stanęła nad samym brzegiem i zauważyła, że od ostatniego skrętu przeszła dokładnie 5 m. Dalej szła wzdłuż brzegu i po 11 metrach stanęła dokładnie na wprost drzewa, znowu w linii prostopadłej do osi rzeki. Wykonała szybko obliczenia i po chwili już wiedziała, jaka była szerokość rzeki. A Ty wiesz?
4. Na osiedlu zainstalowano huśtawki, na których rodzic może bawić się z dzieckiem. Belka huśtawki o długości 2,5 m oparta jest na betonowym słupku o wysokości 60 cm, ale punkt podparcia nie wypada w środku belki, ale dzieli ją w stosunku 1:1,5. Na jaką wysokość wzniesie się na huśtawce dziecko, gdy rodzic dotknie ziemi?
5. Plutonowy Gustaw Jeleń przyłożył oko do muszki karabinu i wystrzelił. Plutonowy ma 182 cm wzrostu i wysokość czoła 12 cm. Po przebyciu drogi o długości 4,1 m pocisk przeszył tarczę na wysokości 80 cm nad ziemią. W jakiej odległości od tarczy należy szukać na ziemi łuski od pocisku?
1. Dziadek Moniki jest zapalonym działkowcem. Właśnie buduje konstrukcję służącą za podporę dla niskopiennej odmiany cukinii. Na płaskim poletku postawił dwie skrzyżowane tyczki i przeciągnął jedną linkę łączącą górne i drugą łączącą dolne końce tych tyczek. Dla upewnienia się, czy wszystko jest w porządku, wykonał kilka pomiarów i zauważył, że iloczyn długości jednej tyczki przez długość części drugiej tyczki od punktu skrzyżowania jednej z linek jest dla obu tyczek taki sam (mierząc do tej samej linki). Na tej podstawie dziadek stwierdził, że linki przebiegają równolegle. Czy miał rację?
2. Dziadek Klaudii również jest zapalonym działkowcem. Właśnie buduje konstrukcję służącą za podporę dla niskopiennej odmiany pieprzu cayenne. W punkty A, B i środek odcinka AB wbił tyczki, tak że ich wspólnym drugim końcem jest C. Następnie przeciągnął równolegle do BC linkę krzyżującą się z tyczką CD w punkcie K, przy czym K dzieli ją w stosunku 1:2, patrząc od dołu. W jakim stosunku koniec tej linki podzielił tyczkę AC?
3. Jak konstrukcyjnie (za pomocą cyrkla i linijki) podzielić koło na 9 części o równych polach?
4. ABCD jest trapezem po podstawach AB i CD, M jest środkiem odcinka AD, kąt MCB ma 150 stopni, BC = x i MC = y. Znajdź pole trapezu ABCD w zależności od x i y.
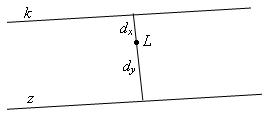 5. Obiekt porusza się po prostej k ze stałą prędkością v. W momencie mijania przez obiekt latarni L agent -0.8 rusza wzdłuż prostej z, poruszając się tak, że dla obiektu będzie cały czas ukryty za latarnią (patrz widok sytuacyjny z pokładu helikoptera H). Naszkicuj wykres zależności prędkości agenta od czasu.
5. Obiekt porusza się po prostej k ze stałą prędkością v. W momencie mijania przez obiekt latarni L agent -0.8 rusza wzdłuż prostej z, poruszając się tak, że dla obiektu będzie cały czas ukryty za latarnią (patrz widok sytuacyjny z pokładu helikoptera H). Naszkicuj wykres zależności prędkości agenta od czasu.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Twierdzenie Talesa - Metoda krokodylka
Twierdzenie Talesa bardzo fajnie można zrozumieć przy pomocy metody krokodylka, którego szczęki spadają na odpowiednie odcinki i obrazują powstawanie proporcji. Metoda jest prosta - a zrozumienie Twierdzenia szybkie.
Więcej zadań z rozwiązaniami wideo z Twierdzenia Talesa można obejrzeć na mojej stronie: MatFiz24.pl:
http://matfiz24.pl/twierdzenie-talesa
Pozdrawiam.
Marek Duda
Tales
Dziękuję Panie Marku,
Poznałam już metodę krokodylka i rzeczywiście jest świetna do opanowania Twierdzenia Talesa. Super pomysł z Panem krokodylem :)
Pozdrawiam.