Z okręgiem Eulera w tle

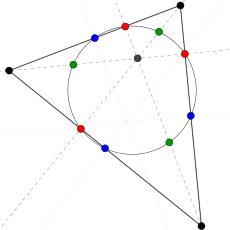
Okrąg Eulera zwany też okręgiem Feuerbacha albo okręgiem dziewięciu punktów jest to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Te punkty to:

• środki boków trójkąta (niebieskie),
• spodki wysokości trójkąta (czerwone),
• punkty dzielące na połowy odcinki, które łączą (czarne) wierzchołki trójkąta z jego ortocentrum, czyli punktem przecięcia prostych zawierających wysokości (zielone).

W 1822 niemiecki geometra Karl Wilhelm Feuerbach - profesor gimnazjum w Erlangen - zauważył, że sześć charakterystycznych punktów trójkąta – środki boków oraz spodki wysokości – leży na jednym okręgu. Niedługo przed nim (1821), ale przy okazji badania geometrii rzutowej, tego samego odkrycia dokonali matematycy francuscy: Charles Brianchon i Jean-Victor Poncelet. Natomiast niedługo później matematyk francuski (pochodzenia żydowskiego) Olry Terquem zauważył i udowodnił, że na wspólnym okręgu leżą też środki odcinków łączących wierzchołki trójkąta z ortocentrum. To Terquem jako pierwszy użył nazwy „okrąg dziewięciu punktów”.

Od tego czasu okrąg ten stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności.  Poniżej rozwiążemy kilka zadań z "dziewięciu punktów" jednak nie korzystając z okręgu Eulera.

Wprowadźmy następujące oznaczenia.

• A, B, C - wierzchołki trójkąta (czarne) leżące przy kątach o miarach odpowiednio α, β, γ i przeciwległe do boków o długościach odpowiednio a, b, c;
• M₁, M_2, M₃ - środki boków trójkąta (niebieskie),
• H₁, H_2, H₃ - spodki wysokości trójkąta (czerwone),
• H - ortocentrum trójkąta (czarne),
• E₁, E_2, E₃ - środki odcinków łączących wierzchołki trójkąta z ortocentrum (zielone),
• O - środek okręgu opisanego na trójkącie,
• R - długość promienia okręgu opisanego na trójkącie,
• I - środek okręgu wpisanego w trójkąt,
• r - długość promienia okręgu wpisanego w trójkąt,
• W₁, W_2, W₃ - punkty przecięcia dwusiecznych kątów trójkąta z okręgiem opisanym na tym trójkącie.

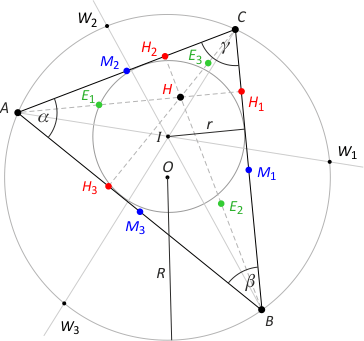
Przypomnijmy też podstawowe fakty geometryczne, z których będziemy korzystać. Każdy z Czytelników z pewnością łatwo je uzasadni.

Fakt 1. Odcinek łączący środki dwóch boków trójkąta (tzw. linia środkowa) jest równoległy do trzeciego boku i dwa razy od niego krótszy.

Fakt 2. Środkowa opuszczona na przeciwprostokątną jest równa jej połowie.

Fakt 3. Odległość wierzchołka trójkąta od ortocentrum jest dwa razy dłuższa od odległości środka okręgu opisanego na tym trójkącie od środka przeciwległego boku.

Zad. 1. Wykaż, że odcinki M₁E₁, M₂E₂, M₃E₃ przecinają się w jednym punkcie, który dzieli je na pół.

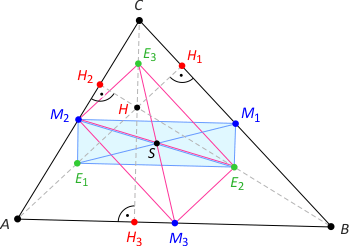
Rozwiązanie. Zauważmy, że odcinki M₂E₁ oraz M₁E₂ są liniami środkowymi odpowiednio w trójkątach AHC i BHC, zatem (z faktu 1) są równoległe do CH i równe jego połowie. Także odcinki M₁M₂ i E₁E₂ są równoległe do AB i równe jego połowie (dlaczego?). Stąd czworokąt E₁E₂M₁M₂ jest równoległobokiem (a nawet prostokątem - dlaczego?), a jego przekątne M₁E₁ i M₂E₂ połowią się nawzajem w punkcie przecięcia S. Analogicznie rozważamy czworokąty E₁M₃M₁E₃ lub M₃E₂E₃M₂.

Zad. 2. Wykaż, że |M₁E₁| = R.

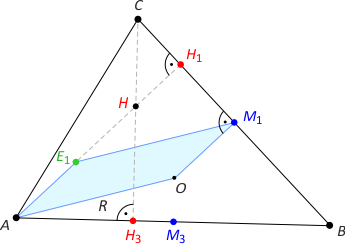
Rozwiązanie. Odcinki AE₁ i OM₁ leżą na prostych prostopadłych do boku BC, więc są równoległe. Z drugiej strony z faktu 3 są równe. Zatem czworokąt AOM₁E₁ jest równoległobokiem stąd teza.

Zad. 3. Wykaż, że |E₁E₂| = |M₁M₂| = |H₁M₃|.

Rozwiązanie. Zauważmy, że odcinek E₁E₂ jest linią środkową w trójkącie AHB, a odcinek M₁M₂ jest linią środkową w trójkącie ABC. Odcinki te z faktu 1 są zatem równe połowie boku AB. Z kolei z faktu 2 w trójkącie prostokątnym ABH₁, środkowa H₁M₃ opuszczona na przeciwprostokątną AB jest od niej dwa razy krótsza. Stąd wynika teza.

Zad. 4. Wykaż, że kąty AE₁H₃ oraz CE₃H₁ mają równe miary.

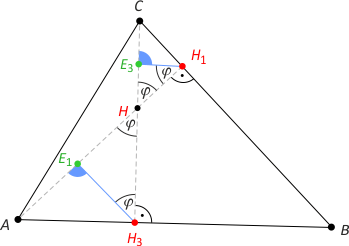
Rozwiązanie. Zauważmy, że z faktu 2 trójkąty E₁H₃H i E₃HH₁ są równoramienne przy czym |∡E₁H₃H| = |∡E₁HH₃| = |∡E₃HH₁| = |∡HH₁E₃| = φ. Kąty AE₁H₃ oraz CE₃H₁ są zewnętrznymi w trójkątach odpowiednio E₁H₃H i E₃HH₁, zatem też mają równe miary.

Zad. 5. Wykaż, że kąt φ między prostymi H₃M₂ i H₂E₃ ma tę samą miarę, co kąt ψ między prostymi H₂M₃ i H₃E₂.

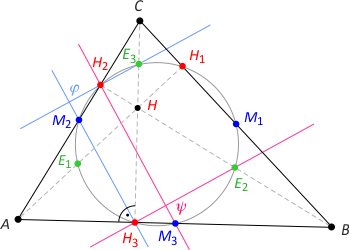
Rozwiązanie. Rozważmy kąty φ i ψ jako zewnętrzne dla odpowiednich trójkątów. Zauważmy, że z faktu 2 w trójkątach AH₃C i CH₂H mamy: |∡AM₂H₃| = 180°–2α oraz |∡CH₂E₃| = 90°–α, stąd φ = 270°–3α. Z drugiej strony z faktu 2 w trójkątach ABH₂ i BHH3 mamy: |∡AM₃H₂| = 180°–2α  oraz |∡E₂H₃B| = 90°–α, stąd ψ = 270°–3α. Stąd wynika teza.

Zad. 6. W trójkącie ABC odcinki BE₁ i H₂M₃ przecinają się w T. Wykaż, że trójkąty H₂E₁T i BM₃T mają równe pola.

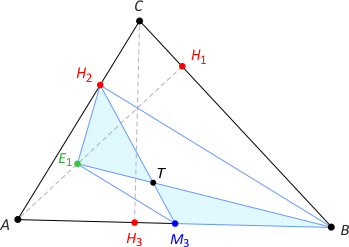
Rozwiązanie. Wystarczy zauważyć, że czworokąt E₁M₃BH₂ jest trapezem, bo odcinek E₁M₃ jest równoległy do BH₂ jako linia środkowa w trójkącie ABH.

Zad. 7. Niech pole czworokąta H₁E₃E₁E₂ wynosi S, a stosunek długości AH do HH₁ wynosi 1,5. Oblicz pole trójkąta ABC.

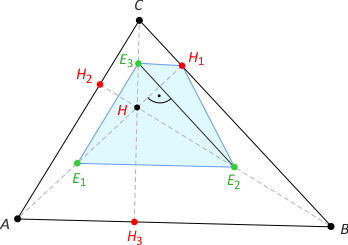
Rozwiązanie. Zauważmy, że E₂E₃ jest prostopadły do AH₁, a stąd S = ¹/₂|E₁H₁|·|E₂E₃|. Z podanego w treści zadania stosunku wynika, że |AH| = ³/₅|AH₁|, skąd |AE₁| = ³/₁₀|AH₁| i dalej |E₁H₁| = ⁷/₁₀|AH₁|. Otrzymujemy zatem S = ¹/₂|E₁H₁|·|E₂E₃| = ¹/₂(⁷/₁₀|AH₁|·¹/₂|BC| = ⁷/₂₀·S_ABC, zatem S_ABC = ²⁰/₇S.

Zad. 8. Wykaż, że |AI|∙|IW₁| = 2Rr.

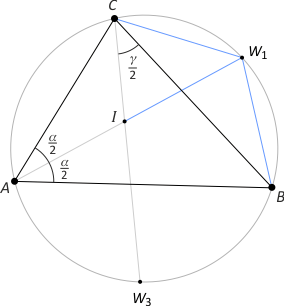
Rozwiązanie. Wykażemy, że |W₁B| = |W₁C| = |IW₁| (jest to tzw. własność trójliścia). Równość pierwsza jest oczywista. Rozważmy trójkąt CIW₁. Mamy |∡ICW₁| = |∡W₃CB| + |∡BCW₁| = ¹/₂(γ+α). Z kolei kąt CIW₁ jest zewnętrzny w trójkącie AIC i ma miarę ¹/₂(γ+α), zatem trójkąt ICW₁ jest równoramienny, przy czym |W₁C| = |IW₁|. Nech CD będzie średnicą okregu opisanego na trójkącie ABC, a K - punktem styczności okręgu wpisanego w ten trójkąt. Zauważmy, że trójkąty prostokątne AIK oraz CDW₁ są podobne z cechy kkk, bo kąty KAI i CDW₁ mają miary α/2. Mamy zatem |KI|:|AI| = |CW₁|:|CD|, skąd po uwzględnieniu, że |KI| = r, a |CD| = 2R i |CW₁| = |IW₁|, mamy tezę.

Zad. 9. Wykaż, że |OI|² = R² – 2Rr (jest to tzw. wzór Eulera).

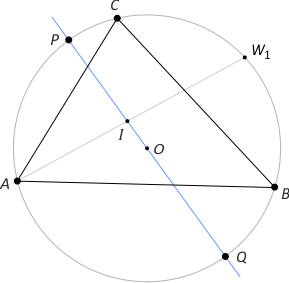
Rozwiązanie. Niech średnica przechodząca przez I przecina okrąg opisany na trójkącie ABC w punktach P i Q. Wówczas z twierdzenia o cięciwach okręgu mamy |AI|·|IW₁| = |PI|·|IQ| = (|PO|–|OI|)·(|OI|+|OQ|) = (R–|OI|)·(R+|OI|) = R²–|OI|². Uwzględniając tezę poprzedniego zadania, mamy |OI|² = R²–2Rr.

Zad. 10. Wykaż, że R ≥ 2r.

Rozwiązanie. Zauważmy, że |OI|² ≥ 0. Stąd i z poprzedniego zadania wynika teza.

Zad. 11. Trójkąt ABC wpisano w okrąg. CD jest średnicą okręgu. Wykaż, że |ID|² = 4R² – ab.

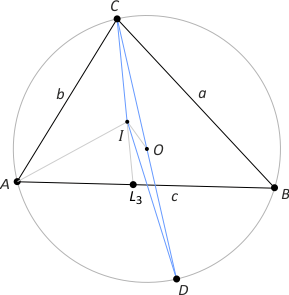
Rozwiązanie. Zauważmy, że OI jest środkową trójkąta CID. Korzystając ze wzoru na środkową, otrzymujemy |OI|² = ¹/₄(2|CI|²+2|ID|²–|CD|²), skąd po uwzględnieniu wzoru Eulera z zad. 9 mamy |ID|² = 4R²–4Rr–|CI|². Korzystając kilkakrotnie z twierdzenia o dwusiecznej kąta wewnętrznego (w trójkątach ABC i AW₃C, po żmudnych przekształceniach otrzymujemy (*) |CI| = (b·|CW₃|) / (b+(bc/(a+b)), gdzie |CW₃| = √(ab–(abc²)/(a+b)²) = (√( ab(a+b–c)(a+b+c)))/(a+b). Po podstawieniu do (*) mamy |CI| = (√ab(a+b–c)(a+b+c))/(a+b+c) = √((ab(a+b–c))(a+b+c)) =√(ab–(2abc)/(a+b+c)) = √(ab–(8RS_ABC)/(2S_ABC/r)) = √(ab–4Rr). Ostatecznie |ID|² = 4R²–4Rr–(ab–4Rr) = 4R²–ab.

Więcej zadań związanych z okręgiem Eurera znajdziecie w artykule Wokół okręgu Eulera.