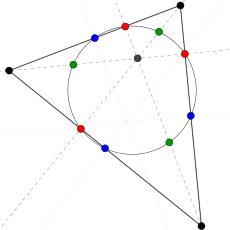
Okrąg Eulera zwany powszechnie okręgiem dziewięciu punktów to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Okrąg ten zrobił niebywałą karierę w geometrii i stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności. O niektórych pisaliśmy już w artykule Z okręgiem Eulera w tle. Teraz poznamy kilkanaście kolejnych.
Przypomnijmy, że okrąg Eulera przechodzi przez dziewięć charakterystycznych punktów dowolnego trójkąta. Te punkty to:
- środki boków trójkąta (niebieskie),
- spodki wysokości trójkąta (czerwone),
- punkty dzielące na połowy odcinki, które łączą (czarne) wierzchołki trójkąta z jego ortocentrum, czyli punktem przecięcia prostych zawierających wysokości (zielone).
Przypomnijmy też podstawowe fakty geometryczne, z których będziemy korzystać. Każdy z Czytelników z pewnością łatwo je uzasadni.
Fakt 1. Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i dwa razy od niego krótszy.
Fakt 2. Środkowa opuszczona na przeciwprostokątną jest równa jej połowie.
Fakt 3. Odległość wierzchołka trójkąta od ortocentrum jest dwa razy większa od odległości środka okręgu opisanego na tym trójkącie od środka przeciwległego boku.
Fakt 4. Trójkąt spodkowy H1H2H3 (o wierzchołkach w spodkach wysokości wyjściowego trójkąta) odcina od trójkąta wyjściowego trzy trójkąty do niego podobne, przy czym |∡H2H1C| = |∡H3H1B| = α, |∡CH2H1| = |∡AH2H3| = β oraz |∡AH3H2| = |∡BH3H1|= γ.
Fakt 5. Na czworokącie wypukłym można opisać okrąg wtedy i tylko wtedy, gdy suma miar przeciwległych kątów wynosi 180°.
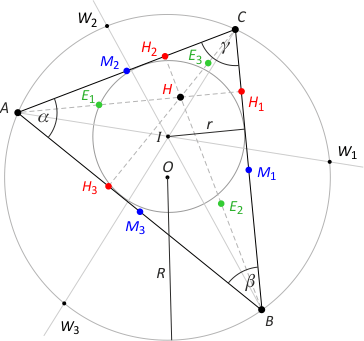
Wprowadźmy standardowe oznaczenia.
- A, B, C - wierzchołki trójkąta (czarne) leżące przy kątach o miarach odpowiednio α, β, γ i przeciwległe do boków o długościach odpowiednio a, b, c;
- M1, M2, M3 - środki boków trójkąta (niebieskie),
- H1, H2, H3 - spodki wysokości trójkąta (czerwone),
- H - ortocentrum trójkąta (czarne),
- E1, E2, E3 - środki odcinków łączących wierzchołki trójkąta z ortocentrum (zielone),
- W1, W2, W3 - punkty przecięcia dwusiecznych kątów trójkąta z okręgiem opisanym na tym trójkącie,
- O - środek okręgu opisanego na trójkącie,
- R - długość promienia okręgu opisanego na trójkącie,
- I - środek okręgu wpisanego w trójkąt,
- r - długość promienia okręgu wpisanego w trójkąt,
- P - pole trójkąta,
- p - połowa obwodu trójkąta.
Zad. 1. Wykaż że |M1M2| = |H1M3|, |H1M2| = |H3M2|, |M1H2|+|M1H3| = |BC|.
Rozwiązanie. Zauważmy, że z faktu 1 mamy |M1M2| = 1/2|AB|, a z faktu 2 w trójkącie ABH1 mamy |H1M3| = 1/2|AB|, czyli |M1M2| = |H1M3|. Dalej z faktu 2 w trójkątach AH1C i AH3C mamy |H1M2| = |H3M2| = 1/2|AC|. Z kolei z faktu 2 w trójkątach BH2C i CH3B mamy |M1H2|+|M1H3| = 1/2|BC| + 1/2|BC| = |BC|.
Zad. 2. Wykaż, że |E1H2| = |OM1|, |M1E2| = |M2E1| = |OM3|.
Rozwiązanie. Z faktu 2 w trójkącie AHH2 mamy |E1H2| = 1/2|AH| = |OM1| ( to ostatnie z faktu 3). Z faktu 1 w trójkątach CHB i AHC mamy |M1E2| = |M2E1| = 1/2|CH| = |OM3| (to ostatnie z faktu 3).
Zad. 3. Wykaż, że M1E2 || M2E1 i M2M1 || E1E2.
Rozwiązanie. Z faktu 1 w trójkątach CHB i AHC mamy M1E2 || M2E1 || CH. Z faktu 1 w trójkątach ABC i AHB mamy M2M1 || E1E2 || AB.
Zad. 4. Wykaż, że |∡M1M2M3| = |∡M2H1H3| i |∡M1M3H1| = |∡H1M2M1|.
Rozwiązanie. Z faktu 1 mamy |∡CM2M1| = α oraz |∡AM2M3| = γ, a stąd |∡M1M2M3| = 180°–α–γ = β. Dalej z faktu 2 w trójkącie AH1C mamy równoramienność trójkąta M2H1C, a stąd |∡M2H1C| = γ. Z kolei z faktu 4 |∡H3H1B| = α. Stąd |∡M2H1H3| = 180°–α–γ = β. Zauważmy teraz , że z faktu 1 mamy |∡M1M3B| = α, a z faktu 2 w trójkącie ABH1 mamy |∡AM3H1| = 2β. Stąd |∡M1M3H1| = 180°–α–2β = γ–β. Z drugiej strony z faktu 2 w trójkącie AH1C mamy |∡CM2H1| = 180°–2γ oraz z faktu 1 mamy |∡AM2M1| = 180°–α. Zatem |∡H1M2M1| = 180°–(180°–2γ) – (180°–α) = γ–β.
Zad. 5. Wykaż (nie korzystając z własności okręgu Eulera) współokręgowość każdej czwórki punktów: M1M2M3H1, M1M2M3E1 oraz H1H2H3M1.
Rozwiązanie.
M1M2M3H1: Z faktu 1 mamy |∡M1M3B| = α oraz |∡M2M3A| = β, a stąd |∡M2M3M1| = 180°–α–β = γ. Z drugiej strony z faktu 2 w trójkącie AH1C mamy równoramienność trójkąta M2H1C, czyli |∡M2H1C| = γ, skąd |∡M2H1M1| = 180°–γ. Na mocy faktu 5 mamy tezę, bo |∡M2M3M1| + |∡M2H1M1| = 180°.
M1M2M3E1: Z faktu 1 w trójkącie AHC odcinek M2E1 jest równoległy do CH, a z faktu 1 w trójkącie ABC odcinek M2M1 jest równoległy do AB. Zatem |∡E1M2M1| = 90°, bo CH jest prostopadłe do AB. Z drugiej strony z faktu 1 |∡M1M3B| = α, a z faktu 1 w trójkącie AHB mamy |∡E1M3A| = 90°–α, skąd |∡E1M3M1| = 90°. Na mocy faktu 5 mamy więc tezę.
H1H2H3M1: Z faktu 4 mamy |∡H2H1C| = α, skąd |∡H2H1M1| = 180°–α. Z drugiej strony z faktu 2 w trójkącie CH3B mamy |∡M1H3B| = β, a z faktu 4 mamy |∡AH3H2| = γ, skąd |∡H2H3M1| = α. Na mocy faktu 5 mamy więc tezę, bo |∡H2H1M1| + |∡H2H3M1| = 180°.
Zad. 6. Wykaż, że punkty C, H2, H3, B są współokręgowe.
Rozwiązanie. Z faktu 2 w trójkątach CH3B i CH2B mamy |M1H2| = 1/2|BC| = |M1H3|, co oznacza, że M1 jest środkiem szukanego okręgu.
Zad. 7. Wykaż, że |BH|·|HH2| = |CH|·|HH3|.
Rozwiązanie. Punkty C, H2, H3 i B są współokręgowe, a BH2 i CH3 są cięciwami tego okręgu przecinającymi się w punkcie H. Na mocy twierdzenia o przecinających się cięciwach mamy tezę. Stanowi ona pewną własność ortocentrum: dzieli ono wysokości trójkąta na odcinki, których iloczyny długości dla danego tyrójkąta są stałe.
Zad. 8. Wykaż, że |∡AH2H3| = |∡ABC|.
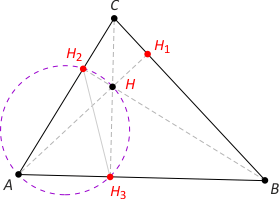
Rozwiązanie. Na mocy faktu 5 na czworokącie AH3HH2 można opisać okrąg. Mamy |∡AH2H3| = |∡AHH3| jako kąty wpisane oparte na tym samym łuku AH3. Z kolei w trójkącie AH3H mamy |∡AHH3| = 90°–|∡HAH3| = 90°–|∡H1AB| = 90°–(90°–β) = β.
Zad. 9. Wykaż, że OA jest prostopadłe do H2H3.
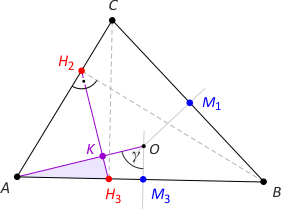
Rozwiązanie. Zauważmy, że |∡AOB| = 2γ (kąt środkowy), skąd |∡AOM3| = γ i |∡OAM3| = 90°–γ. Niech K będzie punktem przecięcia odcinków OA i H2H3. Na mocy faktu 4 mamy |∡H2H3A| = γ = |∡KH3A|. Zatem w trójkącie AKH3 mamy |∡AKH3| = 90°. Analogicznie wzajemnie prostopadłe są pary odcinków OB i H1H3 oraz OC i H2H1.
Zad. 10. Wykaż, że PABC = R·pH, gdzie pH to połowa obwodu trójkąta spodkowego H1H2H3.
Rozwiązanie. Zauważmy, że PABC = PAH3OH2 + PH3OBH1 + PH2OH1C. Korzystając z faktu, że pole czworokata o prostopadłych przekątnych jest równe połowie iloczynu długości tych przekątnych, otrzymujemy PABC = 1/2·|OA|·|H2H3| + 1/2·|OB|·|H1H3| + 1/2·|OC|·|H2H1| = 1/2·R·(|H2H3|+|H3H1|+|H2H1|) = R·pH.
Zad. 11. Wykaż, że ortocentrum jest symetryczne względem spodków wysokości do punktów przecięcia się wysokości z okręgiem opisanym na trójkącie.
Rozwiązanie. Oznaczmy punkt przecięcia prostej zawierającej wysokość CH3 z okręgiem przez H4. Mamy wówczas |∡AH4H1| = |∡AH4C| = |∡ABC| = β. Z drugiej strony |∡AHH3| = β (jak w rozwiązaniu zad. 8). Oznacza to, że trójkąty prostokątne AH3H i AH4H3 są przystające na mocy cechy kbk, bo mają wspólny bok AH3. Stąd wynika teza.
Zad. 12. Wykaż, że pole trójkąta W1W2W3 jest równe 1/2R·p.
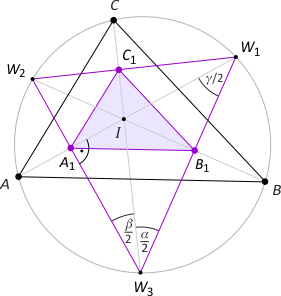
Rozwiązanie. Oznaczmy przez A1 punkt przecięcia dwusiecznej AW1 z odcinkiem W2W3. Rozważmy trójkąt A1W3W1. Mamy |∡A1W3W1| = |∡A1W3I| + |∡IW3W1| = |∡W2W3C| + |∡CW3W1| = |∡W2BC| + |∡CAW1| = β/2 + α/2. Z kolei |∡A1W1W3| = |∡AW1W3| =|∡ACW3| = γ/2. Zatem |∡W1A1W3| = 90°, co oznacza, że A1 jest spodkiem wysokości w trójkącie W1W2W3. Analogicznie punkty B1 i C1 są także spodkami wysokości w tym trójkącie, a punkt I stanowi ortocentrum trójkąta W1W2W3. Stąd trójkąt A1B1C1 jest trójkątem spodkowym trójkąta W1W2W3, zatem na mocy zad. 10 mamy PW1W2W3 = R·pA1B1C1. Mamy też |AA1|=|A1I| i analogicznie |BB1|=|B1I| oraz |CC1|=|C1I|, bo symetryczne odbicie ortocentrum trójkąta leży na okręgu opisanym na tym trójkacie - zad. 11. Zauważmy teraz, że z faktu 1 w trójkątach AIC, AIB oraz BIC mamy 1/2· pABC = pA1B1C1. Stąd wynika teza.
