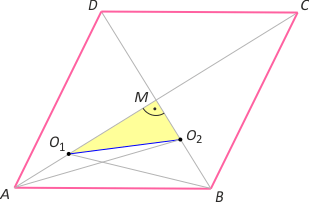
Zad. 1. Środki dwóch okręgów o promieniach R i r są odległe o a. Znajdź długość boku rombu, którego dwa przeciwległe wierzchołki leżą na jednym okręgu, a pozostałe na drugim.
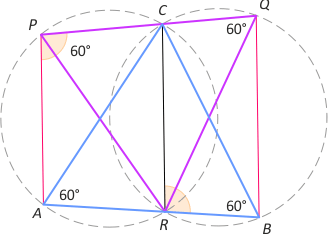
Zad. 2. Dane są dwa trójkąty równoboczne ABC i PQR. Wierzchołek C leży na boku PQ, a wierzchołek R - na boku AB. Wykaż, że AP jest równoległy do BQ.
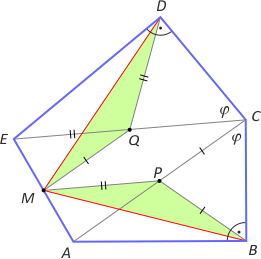
Zad. 3. W wypukłym pięciokącie ABCDE kąty przy wierzchołkach B i D są proste, a kąty BCA i DCE mają równe miary. Niech M będzie środkiem boku AE. Wykaż, że |MB| = |MD|.
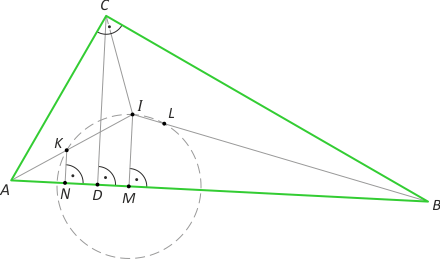
Zad. 4. (wolna amerykanka) W trójkącie ABC kąt C jest prosty, I jest środkiem okręgu wpisanego, a M jest punktem jego styczności z przeciwprostokątną. Okrąg o środku w M przechodzący przez I przecina dwusieczne kątów A i B odpowiednio w punktach K i L (różnych od I). Wykaż, że K i L są środkami okręgów wpisanych odpowiednio w trójkąty ACD i BCD, gdzie CD jest wysokością trójkąta ABC.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Dominik Bysiewicz (student UJ) oraz Filip Derejski (I LO Kraków),
- 20 pkt. - Mikołaj Popek (VIII LO Poznań), Sławomir Matysiak (nauczyciel, X LO Ww),
- 10 pkt. - Jerzy Kawka (I LO Kraków).
Za zadanie 4 komplet 10 pkt. otrzymali: Jacek Bagiński, Dominik Bysiewicz, Tadeusz Porzucek i Adrian Michałowicz (matematyk z Poznania).
Gratulacje!
Zad. 1. Zauważmy, że środki okręgów leżą na symetralnych cięciw BD i AC, w których zawierają się przekątne rombu. Z twierdzenia Pitagorasa w trójkątach O1O2M, AO2M, O1BM oraz ABM otrzymujemy |O1M|2 + |O2M|2 = a2 , |AM|2 = R2 – |O2M|2 , |BM|2 = r2 – |O1M|2 oraz |AB|2 = |AM|2 + |BM|2 = R2 + r2 – a2. Stąd |AB| = √(R2 + r2 – a2).
Zad. 2. Zauważmy, że odcinek CR widać z punktów A i P pod tym samym kątem 60°, stąd na czworokącie ARCP mozna opisać okrąg. Analogicznie na czworokącie CRBQ można opisać okrąg. Mamy zatem |∡APQ| = |∡APC| = |∡CRB| = 180°–|∡CQB| = 180°–|∡PQB|, co oznacza, że AP i BQ są równoległe.
Zad. 3. Niech punkt P będzie środkiem odcinka AC, a punkt Q - środkiem odcinka EC. Wówczas MP i MQ są liniami średnimi w trójkącie EAC oraz |MP|=|EQ| i |MQ|=|PC|. Dalej w trójkątach prostokątnych ABC i ECD mamy |BP|=|PC| oraz |DQ|=|EQ|, bo środkowa przeciwprostokątnej jest od niej dwa razy krótsza. Z drugiej strony z własności linii średniej |∡EQM| = |∡MPA|. Z kolei |∡EQD| = 2φ, bo jest to kąt zewnętrzny dla trójkąta QCD i analogicznie |∡APB| = 2φ. Wynika stąd równość miar kątów MQD i MPB. Zatem na mocy cechy bkb trójkąty MPB i MQD są przystające, skąd |MD|=|MB|.
Zad. 4. (wolna amerykanka) Niech N będzie rzutem prostokątnym punktu K na odcinek AB. Zauważmy, że |KN|:|IM| = |AK|:|AI| = (|AI|–|KI|):|AI| = (|AI|–2|IM|sin(α/2)):|AI|. Ostatnia równość wynika z równoramienności trójkąta KMI, w którym |∡KIM| = 90°– α/2. Dalej mamy |IM| = |AI|sin(α/2) i po podstawieniu |KN|:|IM| = (|AI|–2|AI|sin2(α/2)):|AI| = 1 – 2sin2(α/2) = cosα. Z drugiej strony trójkąty ADC i ABC są podobne w skali |AD|:|AC| = cosα. Pamiętając, że IM jest promieniem okręgu wpisanego w trójkąt ABC, otrzymujemy, że leżący na dwusiecznej kąta A punkt K jest środkiem okręgu wpisanego w trójkąt ADC. Punkt L rozważamy analogicznie.