Zad. 1. Promień okręgu wpisanego w trójkąt wynosi 1/3. Wykaż, że najdłuższa wysokość tego trójkąta jest nie mniejsza od 1.
Zad. 2. Wykaż, że środkowa trójkąta spadająca na jego krótszy bok jest dłuższa od środkowej spadającej na bok dłuższy.
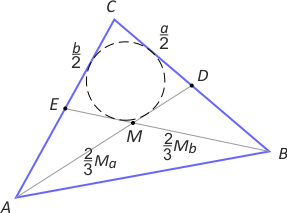
Zad. 3. Niech AD i BE to środkowe w trójkącie ABC, które przecinają się w punkcie M. Wykaż, że jeśli w czworokąt CEMD da się wpisać okrąg, to |AC| = |BC|.
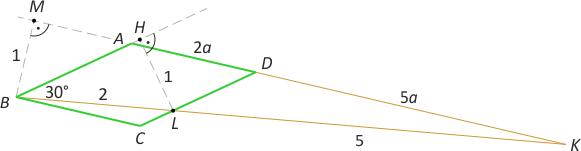
Zad. 4. (wolna amerykanka) W rombie ABCD kąt A jest rozwarty. Na przedłużeniu boku AD poza punkt D obrano punkt K. Odcinki BK i CD przecinają się w punkcie L. Oblicz pole trójkąta ABK, wiedząc, że |BL|=2, |LK|=5, a wysokość rombu wynosi 1.
Za zadania 1-3 punkty otrzymali:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Dominik Bysiewicz (uczeń, I LO Krosno), Jakub Jagiełła (uczeń, LO Politechniki Łódzkiej), Michel Migas (student PW), Karolina Wlaź (studentka UMCS w Lublinie),
- 28 pkt. - Mateusz Kula (student matematyki UŚ),
- 22 pkt. - Adam Wrzesiński (terapeuta z Bielska-Białej)
- 20 pkt. - Tadeusz Porzucek (emerytowany nauczyciel, Gostyń)
- 10 pkt. - Kamil Rozbicki (student WSH we Wrocławiu).
Za zadanie 4 (wolna amerykanka) 10 pkt. otrzymali: Jacek Bagiński, Dominik Bysiewicz, Jakub Jagiełła, Zygmunt Krawczyk (nauczyciel, SLO Żary), Mateusz Kula, Michel Migas, Tadeusz Porzucek, Kamil Rozbicki i Adam Wrzesiński.
Zad. 1. Niech a≤b≤c. Wówczas ha≥ hb≥ hc. Dalej S = a·h/2 = (a+b+c)·r/2. Stąd a·ha = (a+b+c)/3 ≥ 3a/3 = a, czyli ha≥1, co było do okazania.
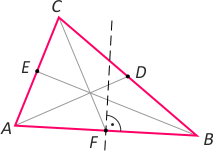
Zad. 2. Niech |BC| > |AC|. Wówczas A i C leżą po jednej stronie symetralnej odcinka AB. Po tej samej stronie leży środkowa CF i środek ciężkości M. Zatem |AM| < |MB|, a stąd |AD| < |BE|.
Zad. 3. Załóżmy nie wprost, że np. |BC| > |AC|. Wówczas (na mocy poprzedniego zadania) |AD| < |BE|. Z założenia w czworokąt EMDC można wpisać okrąg, stąd a/2 + mb/3 = b/2 + ma/3, czyli (a–b)/2 = (ma–mb)/3. Otrzymaliśmy sprzeczność, bo lewa strona jest liczbą dodatnią, a prawa ujemną. Zatem |AC| = |BC|.
Zad. 4. (wolna amerykanka) Niech H będzie rzutem prostokątnym punktu L na prostą AB. Wówczas LH jest wysokością rombu. W trójkącie prostokątnym BHL mamy |BL| = 2 (trójkąt ekierkowy). Z twierdzenia Talesa mamy |AD|/|DK| = 2:5. Niech |AD| = 2a i |DK| = 5a. Wówczas z twierdzenia kosinusów w trójkącie ABK mamy |AK|2 = |AB|2 + |BK|2 – 2|AB|·|BK|·cos30°, a po podstawieniu i przekształceniach: 45a2 +14a√3 – 49 = 0. Rozwiązując to równanie, otrzymujemy a = 7/15 √3. Ostatecznie pole trójkąta ABK wynosi 49/30 √3.