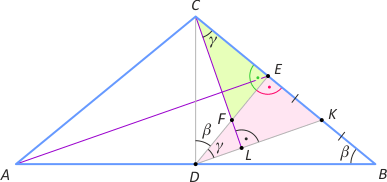
Zad. 1. W pewnym trójkącie |AC| = |BC|. Niech D oznacza środek boku AB, a E - rzut prostokątny D na bok BC. Wykaż, że odcinek AE jest prostopadły do CF, gdzie F jest środkiem odcinka DE.
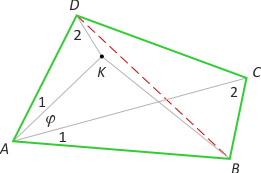
Zad. 2. Wykaż, że jeśli w wypukłym czworokącie ABCD zachodzi równość |AC|·|BD| = |AD|·|BC|+|AB|·|CD|, to czworokąt ten można wpisać w okrąg.
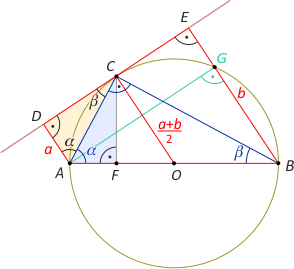
Zad. 3. Dany jest okrąg o średnicy AB. Przez punkt C tego okręgu (różny od A i B) prowadzimy styczną l. Niech D i E będą rzutami prostokątnymi odpowiednio punktów A i B na styczną l. Oblicz odległość punktu C od średnicy AB, wiedząc, że |AD| = a i |BE| = b.
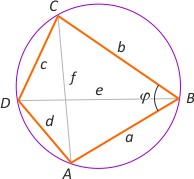
Zad. 4. (wolna amerykanka) W okrąg wpisano czworokąt o bokach a, b, c i d. Oblicz stosunek długości przekątnych tego czworokąta.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Dominik Bysiewicz (student UJ) oraz Jerzy Kawka (I LO Kraków),
- 20 pkt. - Filip Derejski (I LO Kraków),
- 12 pkt. - Mikołaj Popek (VIII LO Poznań),
- 10 pkt. - Michał Malik (I LO Kraków).
Za zadanie 4 komplet 10 pkt. otrzymali: Jacek Bagiński, Dominik Bysiewicz, Tadeusz Porzucek oraz Adrian Michałowicz (matematyk z Poznania).
Gratulujemy!
Zad. 1. Niech K będzie środkiem odcinka EB. Wówczas DK jest równoległy do AF. Niech prosta CF przecina odcinek DK w punkcie L. Wystarczy wykazać, że kąt CLK jest prosty. Zauważmy, że trójkąty prostokątne CDE i DEB są podobne, bo mają wspólny kąt β. Mamy zatem |CE|:|ED| = |ED|:|EB|, a stąd |CE|:1/2|ED| = |ED|:1/2|EB|, co oznacza podobieństwo trójkątów CEF i EDK, przy czym |∡FCE| = |∡EDK|. Na mocy cechy podobieństwa kkk (kąt γ i kąt wspólny przy K) podobne są trójkąty EDK i CLK, a stąd kąt CLK jest prosty, co należało dowieść.
Zad. 2. Niech K będzie takim punktem wewnątrz czworokąta, że |∡DAK| = |∡CAB| oraz |∡ADK| = |∡ACB|. Z podobieństwa trójkątów ADK i ABC mamy |AD|:|AC| = |DK|:|BC|, skąd (*) |AD|·|BC| = |AC|·|DK|. Dalej |∡DAC| = |∡KAB| = (φ+1), skąd na mocy cechy podobieństwa bkb trójkąty AKB i ADC są podobne, bo mamy |AD|:|AC| = |AK|:|AB| oraz kąt φ+1. Zachodzi zatem |KB|:|DC| = |AB|:|AC|, skąd (**) |DC|·|AB| = |KB|·|AC|. Dodając stronami równości (*) i (**), otrzymujemy |KB|·|AC| + |AC|·|DK| = |AC|·(|KB|+|KD|) = |AD|·|BC| + |DC|·|AB| = (z założenia) = |AC|·|BD|, skąd |BD| = |KB|+|KD|, co oznacza, że punkty D, K i B są współliniowe, a |∡ADB| = |∡ACB|. Ostatnia równość oznacza współokręgowość punktów A, B, C i D (twierdzenie odwrotne do twierdzenia o kątach wpisanych opartych na tym samym łuku), co należało dowieść.
Zad. 3. Zauważmy, że czworokąt ABED jest trapezem prostokątnym, a odcinek OC jest jego linią średnią i |OC| = (a+b)/2. Zatem |AB| = a+b. Zauważmy, że kąt AGB jest prosty, a stąd |AG| = |DE|. Z twierdzenia Pitagorasa w trójkącie ABG mamy |AG| = 2√(ab). Dalej zauważmy, że miara kąta dopisanego DCA jest równa mierze kąta ABC. Z podobieństwa trójkątów prostokątnych ACD i ABC mamy równość miar kątów DAC i CAB. Oznacza to, że trójkąty prostokątne ACD i AFC są przystające, przy czym |CF| = |DC| = |DE|/2 = √(ab).
Zad. 4. (wolna amerykanka) Z twierdzenia kosinusów w trójkącie ABC mamy cosφ = (a2+b2–f2)/2ab, a z tego twierdzenia w trójkącie CDA mamy cos(180°–φ) = -cosφ = (d2+c2–f2)/2dc. Stąd (a2+b2–f2)/2ab = (f2–(d2+c2))/2cd. Po przekształceniach otrzymujemy f2 = (ab+cd)(ac+bd)/(ab+dc). Analogicznie rozważając trójkąty DAB i DCB, otrzymujemy e2 = (ab+cd)(ac+bd)/(ad+bc). Ostatecznie e/f = (ab+dc)/(ad+bc).