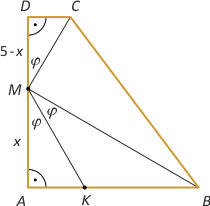
Zad. 1. W trapezie prostokątnym ABCD kąty w wierzchołkach A i D są proste, |AB|=4, |DC|=1 i |AD|=5. Na boku AD obrano punkt M taki, że |∡BMA| = 2|∡CMD|. W jakim stosunku punkt M dzieli bok AD?
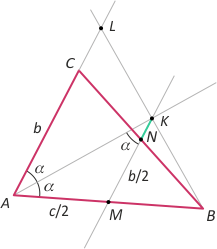
Zad. 2. Niech M i N oznaczają środki boków odpowiednio AB i BC w trójkącie ABC. Dwusieczna kąta A przecina prostą MN w punkcie K. Wykaż, że 2|NK| = ||AC|–|AB||.
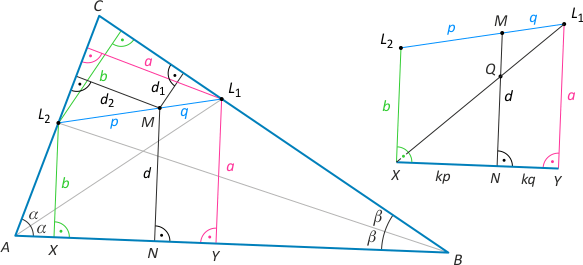
Zad. 3. W trójkącie ABC poprowadzono dwusieczne AL1 i BL2. Wykaż, że odległość dowolnego punktu M odcinka L1L2 od prostej AB równa jest sumie odległości M od prostych AC i BC.
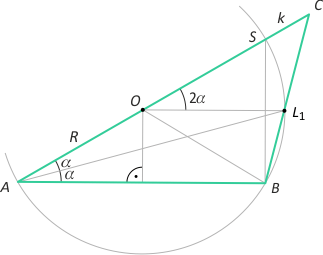
Zad. 4. (wolna amerykanka) W trójkącie ABC poprowadzono dwusieczną AL1. Wiedząc, że |BL1| = 16 i |L1C| = 20, a środek okręgu opisanego na trójkącie ABL1 leży na odcinku AC, znajdź długość boku AB.
Punkty za zadania 1-3 otrzymali:
-
30 pkt. - Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) i Jacek
Bagiński (nauczyciel matematyki, I LO Kraków), - 28 pkt. - Michał Malik (uczeń, I LO Kraków) ,
- 10 pkt. - Filip Derejski (I LO Kraków), Mikołaj Popek (VIII LO Poznań) oraz
Adrian Michałowicz (matematyk z Poznania).
10 punktów za zadanie 4 (wolna amerykanka) otrzymali: Tadeusz Porzucek, Jacek Bagiński, Adrian Michałowicz i Michał Malik.
Gratulujemy!
Zad. 1. Niech MK będzie dwusieczną kąta AMD i niech |AM|=x. Z twierdzenia Pitagorasa w trójkącie ABM mamy |AB| = √(16+x2), a z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy (*) |AK|:|KB| = |AK|:(4–|AK|) = x:√(16+x2) . Z podobieństwa trójkątów prostokątnych DMC i AKM mamy (**) x:|AK| = (5–x):1. Po wyrugowaniu AK z obu równań i prostych przekształceniach otrzymujemy równanie 3x2–25x+48 = 0, skąd x=3, a szukany stosunek wynosi 2/3.
Zad. 2. Niech prosta BK przecina prostą AC w punkcie L. Ze względu na położenie tego punktu rozważymy dwa przypadki. W obu trójkąt AMK jest równoramienny (proste AC i MN są równoległe), a |NK|=|MK|–|MN| lub |NK|=|MN|–|MK|. W obu przypadkach |MK| = c/2, a |MN| = b/2 (jako odcinek łączący środki boków trójkąta ABC). Stąd wynika teza.
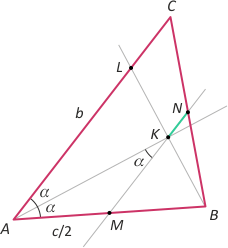
Zad. 3. Niech |L2M| = p i |ML1| = q. Rozważmy trójkąt L2L1C. Mamy a:(p+q) = d2:p, skąd d2 = ap/(p+q) oraz b:(p+q) = d1:q, skąd d1 = bq/(p+q). Z drugiej strony rozważmy trapez XYL1L2. Prosta MN dzieli jego ramiona w tym samym stosunku p:q. Niech Q będzie punktem wspólnym przekątnej trapezu XL1 i prostej MN. Wówczas mamy a/(kp+kq) = |QN|/kp, skąd |QN| = ap/(p+q) oraz b/(p+q) = |QM|/q, skąd |QM| = bq/(p+q). Zatem |MN| = d = |QN| + |QM| = d1 + d2.
Zad. 4. (wolna amerykanka) Niech |SK| = k oraz |∡A| = 2α. Zauważmy, że kąt środkowy L1OS oparty na łuku L1S ma miarę 2α, co oznacza równoległość prostych OL1 i AB. Z twierdzenia Talesa otrzymujemy BL1:L1C = AO:OC = R/(R+k) = 4/5, a stąd R=4k. Dalej z twierdzenia o potędze punktu mamy |CS|·|CA| = |CL1|·|CB| lub inaczej |CL1|(|CL1|+|L1B|) = k(k+2R) i ostatecznie 20(20+16) = 9k2, skąd k=4√5. Dalej z twierdzenia sinusów w trójkącie ABL1 mamy BL1/sinα = 32√5, skąd sinα = √5/10. Z "jedynki trygonometrycznej" otrzymujemy cosα = √95/10. Rozważmy teraz trójkąt prostokątny ABS. Mamy |AB| = |AS|·cos2α = 2R·cos2α = (32√5)·(cos2α–sin2α) = (32√5)·(95/100–5/100) = (144√5)/5.