Zad. 1. W trapezie suma kątów przy dłuższej podstawie jest kątem prostym. Oblicz długość odcinka łączącego środki podstaw, wiedząc, że wartość bezwzględna różnicy długości podstaw wynosi 4.
Zad. 2. Znajdź takie dwie liczby naturalne, by ich różnica wynosiła 66, zaś najmniejsza wspólna wielokrotność była równa 360.
Zad. 3. Czy równanie x2 + y2 = xy + 2 ma rozwiązania w parach liczb całkowitych?
W listopadzie punkty zdobyli:
- 3 pkt. – Maksymilian Skica G-Akademickie PWr, Joanna Galik SP 5 Wrocław, Mateusz Kotarba SP 2 Świątniki Górne, Kacper Woszczek PSP Mieroszów, Wojciech Szwarczyński PSP Kowalowa, , Piotr Zug SP 1 Borki Wielkie, Jerzy Wąsiewicz Publiczna Katolicka SP Magdalenka, Hubert Bączyk G 1 Swarzędz, Marta Sibielec G 48 Wrocław, Gabriela Pietras PSP Leszczyna, Laura Stefanowska G Legnica, Kosma Kasprzak G 58 Poznań, Agata Lefler ZSS Wołów, Tomasz Lefler ZSS Wołów, Wiktoria Cymerman G-Europejskie Zgorzelec, Maksymilian Szczepaniak SP Siechnice, Kuba Domagała G 1 Swarzędz, Angelika Goska G Rzeczyca i Igor Wojtasik SP11 Jelenia Góra;
- 2 pkt. – Bartosz Nodzak SP 152 Łódź, Maksymilian Szczepaniak SP Siechnice, Patrycja Rogulska, Oliwer Rum PG 1 Głogówek, Jakub Perek G Rzeczyca, Jan Podlasek G Rzeczyca;
- 1 pkt – Jakub Dubiel SP 5 Wrocław.
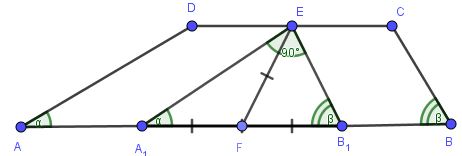
Zad. 1. Niech E i F oznaczają środki podstaw trapezu ABCD (odpowiednio DC i AB). Z punktu E prowadzimy proste równoległe do ramion. Przetną one podstawę AB odpowiednio w punktach A1 i B1. Z warunków zadania wynika, że A1EB1 jest trójkątem prostokątnym. EF jako środkowa poprowadzona z wierzchołka kąta prostego ma długość równą połowie długości przeciwprostokątnej A1B1 (jest długością promienia okręgu opisanego na trójkącie).
Mamy |A1B1| = |AB|–|AA1|–|B1B|= |AB|–|DE|–|EC| = |AB|–|DC|= 4. Ostatecznie |EF| = 1/2·4 = 2.
Zad. 2. Oznaczmy szukane liczby przez x i y. Spełniają one warunki x–y = 66 oraz NWW(x, y) = 360. Zatem istnieją takie liczby naturalne m i n (różne od 0) względnie pierwsze, że mx = 360 i ny = 360.
Stąd x = 360/m i y = 360/n.
Podstawiając do równania x–y = 66 i przekształcając, otrzymujemy
1/m – 1/n = 11/60 . 60 = 1 . 60 = 2 . 30 = 4 . 15 = 5 . 12 = 6 . 10 oraz 15 – 4 = 11.
Zatem m = 4, n = 15. Ostatecznie szukane liczby to x = 90, y = 24.
Zad. 3. Dane równanie jest równoważne równaniu 4x2 – 4xy + 4y2 = 8 i dalej równaniu (2x–y)2 + 3y2 = 8. Jeżeli to równanie ma rozwiązanie w parach liczb całkowitych, to 3y2≤ 8, a więc y=0 lub y=1. Żaden z tych przypadków nie zachodzi, ponieważ wtedy x nie jest całkowite, zatem równanie jest sprzeczne.







