Zad. 1. Od sześcianu odcięto rogi w ten sposób, że w miejscu każdego starego wierzchołka powstała ściana w kształcie równobocznego trójkąta. Jeżeli wierzchołki nowej bryły połączymy odcinkami każdy z każdym, to ile z tych odcinków będzie leżało wewnątrz powstałego ściętego sześcianu?
Zad. 2. Cylindryczna beczka o średnicy 1 m leży na boku tuż przy ścianie. W wolnej przestrzeni między beczką, podłogą i ścianą mieści się dokładnie piłka. Jaką ma średnicę?
Zad. 3. Na ile sposobów można wybrać k pól szachownicy n × n (n>k) tak, aby żadne dwa z wybranych pól nie leżały ani w jednym wierszu, ani w jednej kolumnie?
W listopadzie punkty zdobyli:
- 3 – Emilia Cichowska II LO Lubin, Urszula Derkacz SP XL Warszawa, Michał Węgrzyn ALO PWr Wrocław;
- 2 – Artur Bumażnik ZSE Jelenia Góra, Aleksander Kiszkowiak I TE Warszawa, Ewa Kucharska I LO Leszno, Miłosz Zakrzewski LO Tuchola;
- 1 – Paulina Budnik Uniwersyteckie XII LO Olsztyn, Jakub Garbaczewski II LO Oleśnica, Konrad Kocwin I LO Jawor, Karolina Szymandera I LO Inowrocław, Igor Wojtasik I LO Jelenia Góra.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. W miejsce każdego starego wierzchołka powstają trzy nowe. Łącznie sześcian ścięty ma 8·3 = 24 wierzchołki (jak na diagramie poniżej).
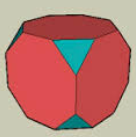
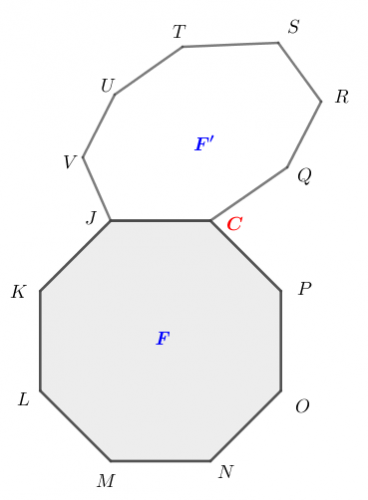
Każdy wierzchołek leży na jednej ze starych krawędzi, czyli na dwóch starych kwadratowych ścianach. Popatrzmy na jeden z wierzchołków ozn. C, który należy do ścian F i F’ (patrz diagram poniżej). Punkt C jest połączony krawędziami z dokładnie trzema wierzchołkami J, P, Q. Przekątne ośmiokątnej ściany F łączące C z każdym z innych pięciu wierzchołków należących do tej ściany (czyli z punktami K, L, M, N, O) leżą na powierzchni ściętego sześcianu, podobnie jak przekątne ściany F’ łączące C z pięcioma wierzchołkami należącymi F’. Pozostałe odcinki łączące C z 24–1–3–(2.5) = 10 innymi wierzchołkami bryły leżą wewnątrz sześcianu ściętego. To samo dotyczy każdego z 24 wierzchołków. Łącznie otrzymamy 24.10 = 240 takich odcinków, ale każdy z nich liczymy w tym procesie dwukrotnie (dlaczego?), więc szukana liczba odcinków wynosi 120.
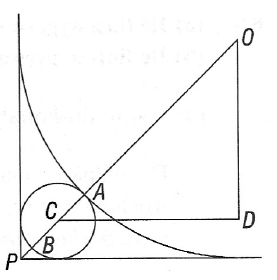
Zad. 2. Sytuację opisaną w zadaniu narysujmy w przekroju płaszczyzną prostopadłą do ściany. Na rysunku poniżej P jest punktem, w którym ściana styka się z podłogą, O jest środkiem przekroju poprzecznego beczki, C - środkiem piłki, a A i B są punktami, w których odcinek OP przecina odpowiednio beczkę i piłkę. Odcinek OD jest równoległy do ściany, a CD - do podłogi. Odcinki OD i CD są wzajemnie prostopadłe i równe (dlaczego?). Oznaczmy przez r i R promienie odpowiednio piłki i przekroju beczki. Wówczas |OC| = R+r i |CD| = |OD| = R–r. Na mocy twierdzenia Pitagorasa dla trójkąta OCD otrzymujemy (R+r)2 = 2(R–r)2, czyli R+r = √2(R–r). Podstawiając R = 0,5, otrzymujemy 0,5+r = √2(0,5–r), skąd 2r = 3–2√2 ≈ 0,1715 i to jest średnica piłki w metrach, co daje 17,15 cm.
Zad. 3. Z n wierszy można wybrać k na [tex]{{n}\choose{k}}[/tex] sposobów. W pierwszym z wybranych wierszy kolumnę można wybrać na n sposobów, w drugim na n-1 sposobów, w trzecim na n-2, …, w k-tym - na n-k+1 sposobów. Stąd liczba wszystkich sposobów wybrania k pól zgodnie z warunkami zadania wynosi [tex]{{n}\choose{k}}n(n-1)(n-2)...(n-k+1)={{n}\choose{k}}\frac{n!}{(n-k)!}[/tex].







