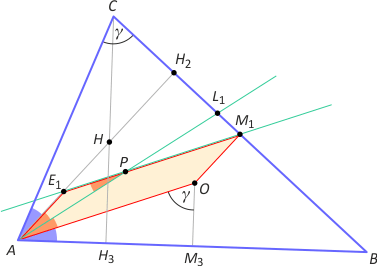
Zad. 1. W trójkącie ABC poprowadzono dwusieczną AL1, która przecina w punkcie P prostą M1E1, gdzie M1 jest środkiem boku BC, E1 - środkiem odcinka AH, a H to ortocentrum trójkąta. Wykaż, że trójkąt APE1 jest równoramienny.
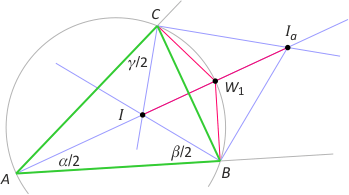
Zad. 2. Wykaż, że |IW1| = |CW1| = |BW1| = |W1Ia|, gdzie W1 jest punktem przecięcia okręgu opisanego na trójkącie ABC z dwusieczną kąta A, I jest środkiem okręgu wpisanego w ten trójkąt, a Ia oznacza środek okręgu dopisanego do trójkąta, stycznego do boku BC.
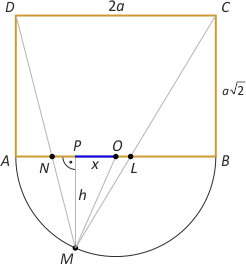
Zad. 3. W prostokącie ABCD mamy |AB|= 2a i |BC|= a√2. Na boku AB jako na średnicy zbudowano półokrąg. Niech M jest dowolnym punktem tego półokręgu (różnym od końców średnicy). Proste MD i MC przecinają bok AB w punktach odpowiednio N i L. Oblicz wartość |AL|2 + |BN|2.
Zad. 4. (wolna amerykanka) Wykaż, że pole trójkąta ABC jest równe 1/2|AW1|·|MN|, gdzie M i N są rzutami prostokątnymi spodka L1 dwusiecznej kąta A na boki AC i AB, a W1 jest punktem przecięcia okręgu opisanego na trójkącie ABC z dwusieczną kąta A.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 pkt. - Dominik Bysiewicz (student UJ), Jerzy Kawka (I LO Kraków), Mikołaj Popek (VIII LO Poznań),
- 10 pkt. - Filip Derejski (I LO Kraków).
W kategorii "wolnej amerykanki" 10 punktów otrzymali: Jacek Bagiński, Dominik Bysiewicz, Adrian Michałowicz (matematyk z Poznania) i Tadeusz Porzucek.
Gratulacje!
Zad. 1. Zauważmy, że czworokąt AOM1E1 jest równoległobokiem, bo odcinek AE1 jest równoległy i przystający do odcinka OM1 (uzasadnienie: zadanie 3, maj 2015). Zatem |∡E1PA| = |∡PAO|, bo to są kąty naprzemianległe, i |∡PAO| = |∡E1AP|, z definicji dwusiecznej. Stąd wynika teza.
Zad. 2. Równość długości odcinków W1B i W1C jest oczywista. Kąt CIW1 jest zewnętrznym dla trójkąta AIC, więc ma miarę α/2+γ/2, a kąt ICW1 jest sumą kątów ICB oraz BCW1 i też ma miarę α/2+γ/2. Oznacza to, że trójkąt ICW1 jest równoramienny, przy czym |IW1|=|W1C|. Rozważmy teraz trójkąt BW1A. Mamy |∡W1IaB| = |∡AIaB| = 180°–α/2–β–(180°–β)/2 = γ/2 oraz |∡W1BIa| = 90°–β/2–|∡CBW1| = 90°–β/2–α/2 = γ/2. Oznacza to, że trójkąt W1BIa jest równoramienny i |W1B| =|W1Ia|.
Zad. 3. Zauważmy podobieństwo trójkątów DAN i NMP w skali a√2 : h. Stąd odcinek AP o długości a–x jest podzielony na dwie części w tym właśnie stosunku, skąd |AN| = ((a–x)·a√2) : (a√2+h). Dalej |BN| = 2a–|AN| = (a√2(a+h√2 +x)) : (h+a√2). Analogicznie z podobieństwa trójkątów PML i LBC wynika podział odcinka PB na dwie części w stosunku a√2 : h. Mamy zatem |BL| = ((a√2)(a+x)) : (h+a√2), skąd |AL| = 2a–|BL| = (a√2(a+h√2–x)) : (h+a√2). Z twierdzenia Pitagorasa w trójkącie prostokątnym OPM otrzymujemy h = √(a2–x2). Ostatecznie (po dość żmudnych przekształceniach) otrzymujemy |AL|2 + |BN|2 = 4a2.
Zad. 4. (wolna amerykanka) Zauważmy, że na czworokącie ANL1M można opisać okrąg (suma miar kątów o wierzchołkach w M i N wynosi 180°) o średnicy AL1. Z twierdzenia sinusów w trójkącie AMN mamy |MN| = |AL1|sinα. Punkt W1 jest środkiem łuku BC, więc średnica W1D jest prostopadła do boku BC, a tym samym równoległa do wysokości AH1. Oznacza to, że kąty H1AL1 i AW1D mają równe miary, a trójkąty AH1L1 i AW1D są podobne. W trójkącie AW1D mamy |AW1| = 2Rcosφ, a w trójkącie AH1L1 mamy |AH1| = |AL1|cosφ. Ostatecznie 1/2·|MN|·|AW1| = 1/2·|AL1|sinα·2Rcosφ = 1/2·|AH1|·|BC| = SABC.








