Zad. 1. Przez wierzchołek czworokąta wypukłego poprowadź prostą dzielącą go na dwie części o równych polach.
Zad. 2. Niech A', B' i C' oznaczają odpowiednie spodki wysokości opuszczonych z wierzchołków trójkąta ostrokątnego ABC. Niech K i L oznaczają rzuty prostokątne C' na proste AC i BC. Wykaż, że prosta KL połowi odcinki C'A' i C'B'.
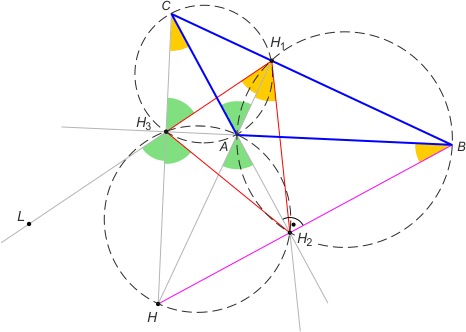
Zad. 3. Wykaż, że punkt przecięcia prostych zawierających wysokości trójkąta rozwartokątnego, jest środkiem okręgu dopisanego do trójkąta, którego wierzchołkami są spodki wysokości trójkąta wyjściowego.
Zad. 4. (wolna amerykanka) Wewnątrz trójkąta ABC dany jest dowolny punkt P. Wykaż, że z odcinków o długościach |PA|sinα, |PB|sinβ oraz |PC|sinγ można zbudować trójkąt.
Za rozwiązania zadań 1-3 punkty zdobyli:
- 30 pkt. - Robert Ciężabka (student AGH Kraków ), Michel Migas (student PW ), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń) oraz Paweł Wesołowski (uczeń II LO Końskie),
- 20 pkt. - Mikołaj Sikora (uczeń III LO Tarnów) i Sabina Khady Sy (studentka UJ),
- 10 pkt - Szymon Kaźmierowski (nauczyciel, IV LO Elbląg ).
Za zadanie 4 punkty otrzymali:
- 10 pkt. - Robert Ciężabka, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora i Sabina Khady Sy,
- 2 pkt. - Wojciech Tomiczek (inżynier, Lipowa).
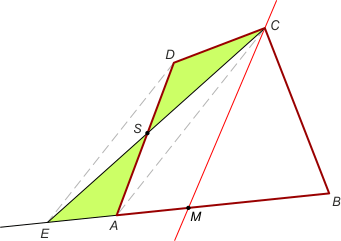
Zad. 1. Poprowadźmy przez wierzchołek D prostą równoległą do przekątnej AC i niech przecina ona prostą AB w punkcie E. Łatwo zauważyć, że pole trójkąta EBC jest równe polu czworokąta ABCD. Szukana prosta przechodzi przez środek M boku EB.
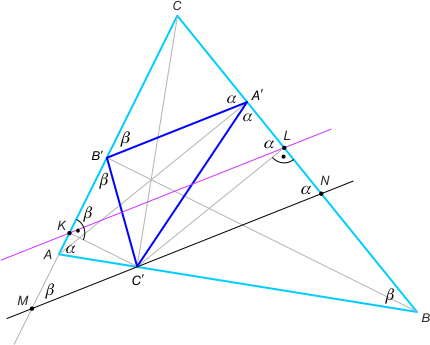
Zad. 2. Skorzystamy z faktu, że A'B' oraz KL są równoległe, wszak oba te odcinki tworzą z AC kąt β (A'B' - bo jest antyrównoległe do AB - patrz zad. 2, październik 2014, a |∡CKL|= β jak w zad. 3, listopad 2015). Niech punkt M na prostej AC będzie symetryczny do B' względem K, a punkt N na prostej BC - symetryczny do A' względem L. Wówczas prosta KL jest linią średnią w trójkątach równoramiennych MC'B' i C'BA'. Stąd teza.
Zad. 3. Wystarczy wykazać, że CH i HH1 są odpowiednio dwusiecznymi kątów LH3H2 i H3H1H2. Skorzystamy z faktu, że na czworokątach H3HH2A, H3AH1C oraz AH2BH1 można opisać okręgi (przeciwległe kąty są proste). Zauważmy wówczas, że |∡LH3H| = |∡CH3H1| (kąty wierzchołkowe), a to dalej jest równe |∡CAH1| (kąty wpisane oparte na łuku CH1), to z kolei jest równe |∡HAH2| (kąty wierzchołkowe), a to jest równe |∡HH3H2| (kąty wpisane oparte łuku HH2).
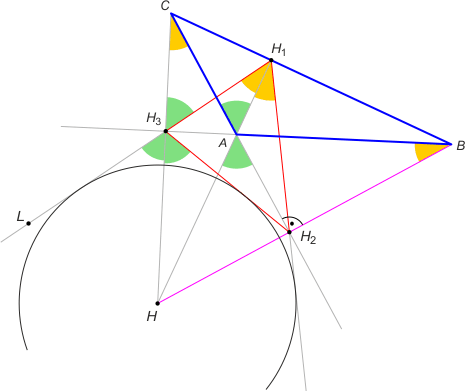
Z drugiej strony |∡H3H1A| = |∡H3CA| (kąty wpisane oparte na łuku H3A), to dalej jest równe |∡ABH2 | (z podobieństwa trójkątów prostokątnych H3AC oraz AH2B), a to z kolei jest równe |∡AH1H2| (kąty wpisane oparte na łuku AH2). Zatem punkt H jest środkiem okręgu dopisanego do trójkąta H3H2H1.
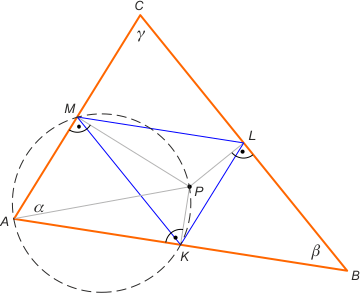
Zad. 4. (wolna amerykanka) Zauważmy, że na czworokącie AKPM można opisać okrąg, którego średnicą jest AP. Z twierdzenia sinusów w trójkącie AKM mamy |MK| = |AP|·sinα. Analogicznie |ML| = |CP|sinγ oraz |KL| = |BP|sinβ. To kończy dowód, bo szukanym trójkątem jest KLM.