Zad. 1. Prosta PA jest styczna do okręgu w punkcie A. Cięciwa BC jest równoległa do PA. Proste PB i PC przecinają okrąg w punktach odpowiednio K i L. Wykaż, że prosta KL połowi odcinek PA.
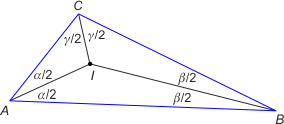
Zad. 2. W trójkącie połączono środek okręgu wpisanego z wierzchołkami. Otrzymano trzy mniejsze trójkąty z których jeden jest podobny do trójkąta wyjściowego. Oblicz miary jego kątów.
Zad. 3. Dany jest równoległobok ABCD. Na boki DC i BC (lub ich przedłużenia) opuszczono wysokości odpowiednio AM i AN. Wykaż, że trójkąty ADC i MAN są podobne.
Zad. 4. (wolna amerykanka) Pole trójkąta ABC wynosi 15√3. Kąt A ma 120°, a kąt B jest większy niż kąt C. Odległość wierzchołka A od środka okręgu wpisanego w trójkąt ABC wynosi 2. Oblicz długość środkowej BD.
Za rozwiązanie zadań kwietniowych maksymalną liczbę 30 punktów otrzymali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Sławomir Matysiak (nauczyciel, ZS nr 1 Trzebnica), Michel Migas (student PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca nr 131 Charków, Ukraina). 20 punktów zdobyli: Iwona Gruszecka (nauczyciel, G 42 Warszawa) i Zygmunt Krawczyk (nauczyciel, SLO Żary).
W kategorii "wolna amerykanka" 10 punktów zdobyli: Jacek Bagiński, Włodzimierz Bąk, Michel Migas, Zygmunt Krawczyk, Tadeusz Porzucek, Mikołaj Szamajew oraz Sabina Sy (studentka UJ) i Wojciech Tomiczek (inżynier, Lipowa)
Gratulujemy!
Zad. 1. Wystarczy wykazać, że |PM|2 = |MA|2. W czworokącie KBCL kąt BCL ma miarę φ i przystaje do kąta MPL jako naprzemianległy, bo BC jest równoległe do PA. Ponieważ czworokąt KBCL jest wpisany w okrąg, kąt BKL ma miarę 180°–φ, a PKL (jako przyległy) ma miarę φ. Wynika stąd, że trójkąty PLM i PKM są podobne, bo mają jeszcze wspólny kąt PMK. Otrzymujemy proporcję |PM|/|ML| = |MK|/|PM|, skąd |PM|2 = |ML|·|MK|. Także trójkąty MAL i MKA są podobne, bo mają wspólny kąt KMA, a dopisany kąt MAL jest oparty na tym samym łuku, co kąt
wpisany LKA, więc mają równe miary. Stąd mamy proporcję |MA|/|ML| = |MK|/|MA|, czyli |MA|2 = |ML|·|MK|. Z obu otrzymanych równości wynika już teza.

Zad. 2. Niech np. α/2 = β oraz γ/2 = α. Wówczas |∡AIC| = 180° – α/2 – γ/2 = γ. Po podstawieniu otrzymujemy 180° – α/2 – α = 2α, skąd α = 2π/7, β = π/7 oraz γ = 4π/7.
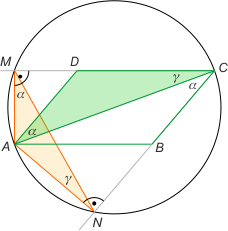
Zad. 3. Zauważmy, że na czworokącie ANCM można opisać okrąg, bo |∡ANC| = |∡AMC| = 90°. Kąty DCA i MNA są przystające, jako wpisane oparte na łuku MA. Także kąty AMN i DAC są przystające, bo DAC jest naprzemianległy do ACB, a ten jest oparty na łuku AN podobnie jak kąt AMN. Zatem trójkąty ANM i
ADC są podobne.
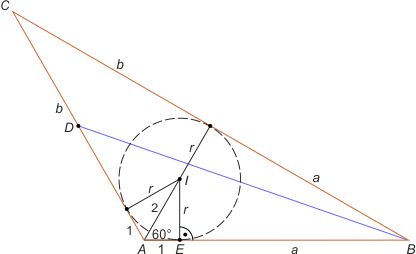
Zad. 4. (wolna amerykanka) W trójkącie ekierkowym AEI zachodzi |AI| = 2, stąd |AE| = 1 oraz |IE| = r = √3. Zatem obwód trójkąta ABC wynosi 2PABC/r = 30. Stąd mamy 2a + 2b + 2 = 30 i dalej a + b = 14. Wystarczy teraz
rozwiązać układ równań a + b = 14 i (a+1)(b+1)·sin120° = 15√3. Jest on spełniony przez parę (a, b) = (5, 9). Korzystając z twierdzenia kosinusów w trójkącie ABC, otrzymujemy |BD|2 = |AD|2 + |AB|2 – 2|AD|·|AB|·cos120° = 52 + 62 –2·5·6·(-1/2), a stąd |BD| = √91.