Torus

Definicja geometryczna:
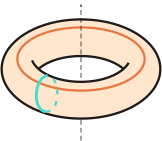
Torus (lub torus pierścieniowy) to dwuwymiarowa powierzchnia obrotowa powstała w wyniku obrotu o kąt pełny okręgu wokół prostej znajdującej się w płaszczyźnie tego okręgu oraz rozłącznej z nim.

Definicja topologiczna:
Powierzchnia dwuwymiarowa powstała przez utożsamienie (sklejenie) brzegów prostokąta: najpierw sklejamy boki przeciwległe, otrzymując powierzchnię boczną walca, a następnie sklejamy otrzymane na brzegu okręgi.

Modele rzeczywiste:

• dętka rowerowa
• obwarzanek
• pączek amerykański (doughnut)

Przykłady niestandardowych torusów geometrycznych:

• Torus wrzecionowy - nie ma pierściennego kształtu, powstaje z obrotu okręgu wokół prostej do niego stycznej i leżącej w jego płaszczyźnie. W sensie topologicznym jest to jednopunktowa suma dwóch sfer.
  rysunek plik
• Torus rogaty - nie ma pierściennego kształtu, powstaje z obrotu okręgu wokół jego siecznej. W sensie topologicznym jest to dwupunktowa suma dwóch sfer.

  rysunek plik

Przykłady torusów topologicznych:

• Torus eliptyczny - powstaje z obrotu elipsy wokół osi z nią rozłącznej, ale leżącej w jej płaszczyźnie.
• Torusy wielokątne - powstają z obrotu wielokąta wokół osi z nim rozłącznej, ale leżącej w jego płaszczyźnie. Więcej można o nich przeczytać na Portalu w dziale MAT-ŚWIAT w artykule Zakręcone graniastosłupy (1) i (2).
  animacja z matświata
• Toroidy - o ile powstają z obrotu dowolnej krzywej płaskiej, zwyczajnej i zamkniętej wokół osi rozłącznej z tą krzywą, ale leżącej w jej płaszczyźnie (krzywa nie może mieć samoprzecięć).
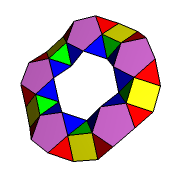
  animacja z mat-świata
• Wielościany toroidalne - powierzchnie z genusem 1 (tzn. zawierające jedną "dziurę") ograniczone wielokątami, są torusami w sensie topologicznym, choć nie są w sensie geometrycznym.

Kontrprzykłady:

• Powierzchnie zwane cytryną i jabłkiem - powstają z obrotu łuku okręgu (odpowiednio mniejszego lub większego od półokręgu) wokół cięciwy łączącej końce tego łuku; nie są torusami w sensie geometrycznym, bo nie powstają z obrotu okręgu. W sensie topologicznym są to sfery.
  rysunek plik

• Torus podwójny oraz n-torusy (czyli powierzchnie z dwoma lub n dziurami) nie są torusami topologicznymi, gdyż mają genus większy niż 1, a on jest niezmiennikiem topologicznym.

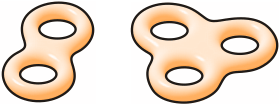
• Torus niemożliwy jest figurą, która nie istnieje w przestrzeni trójwymiarowej.

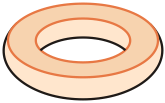
Elementy składowe torusa:

• Każdy okrąg otrzymany w przekroju torusa płaszczyzną zawierającą jego oś symetrii obrotowej to południk.

• Każdy okrąg otrzymany w przekroju torusa z płaszczyzną prostopadłą do jego osi symetrii obrotowej to równoleżnik.
  

Własności geometryczne:

• Torus to powierzchnia dwuwymiarowa leżąca w przestrzeni trójwymiarowej.
• Torus pierścieniowy (a także eliptyczny i wielokątny) jest szczególnym przypadkiem toroidu.
• Wszystkie południki torusa są przystające, a równoleżniki nie.
• Przez każdy punkt na torusie przechodzą cztery okręgi w całości leżące na tym torusie: południk, równoleżnik i 2 okręgi Villarceau [czytaj: łilarsou].

• Pole powierzchni wynosi 4π²rR, gdzie r to promień okręgu będącego południkiem torusa, a R to odległość jego środka od osi obrotu.
• Objętość bryły ograniczonej przez torus wynosi 2π²r²R, gdzie r to promień okręgu będącego południkiem torusa, a R to odległość jego środka od osi obrotu.
• Maksymalna liczba części, jakie można otrzymać, rozcinając torus n płaszczyznami to ¹/₆(n³+3n²+8n). Dla cięć, w których liczba płaszczyzna zmienia się od 1 do 10 wartości te wynoszą 2, 6, 13, 24, 40, 62, 91, 128, 174 i 230.

Własności topologiczne:

• Torus jest powierzchnią dwustronną (orientowalną) bez brzegu.
• Torus jest rozmaitością topologiczną, czyli powierzchnią, która jest lokalnie euklidesowa (to znaczy, że otoczenie każdego punktu jest dyskiem).
• Krzywa zwyczajna zamknięta na torusie może należeć do jednej z trzech klas. Może być ściągalna do punktu, ściągalna do południka lub ściągalna do równoleżnika.
• Topologicznie torus jest równoważny sferze z jedną rączką, torus podwójny - sferze z dwiema rączkami itd.
  

• Genus g torusa (czyli liczba całkowita charakteryzująca powierzchnie topologiczne równa liczbie "otworów" w tej powierzchni) wynosi 1.
• Charakterystyka Eulera χ torusa (czyli liczba 2-2g, gdzie g to genuspowierzchni) wynosi 0.
• Najprostszą formą wielościenną równoważną topologicznie torusowi (tzn. powierzchnią z genusem 1 ograniczoną wielokątami tzw. wielościanem toroidalnym) jest wielościan Szilassiego, który ma tylko 7 ścian, każda granicząca z każdą.
• Do pokolorowania dowolnej mapy na torusie tak, aby sąsiadujące kraje miały inne barwy potrzeba aż 7 kolorów (na płaszczyźnie i sferze wystarczą 4). Przykładem na to, że 6 barw to za mało, jest np. takie kolorowanie wielościanu Szilassiego, w którym każda ściana to inne państwo.
• Na torusie można ułożyć bez samoprzecięć graf pełny o 6 wierzchołkach tzn. sześć punktów można połączyć każdy z każdym liniami, które się nie przecinają (na płaszczyźnie i sferze takich punktów może być tylko 4).

• kartezjańskie - jeżeli za oś obrotu przyjmiemy oś OZukładu współrzędnych OXYZ,natomiast okrąg o środku (R, 0, 0) i promieniu r (gdzie 0<R, 0<r<R) umieścimy w płaszczyźnie y=0, to równanie torusa powstałego z obrotu tego okręgu wokół tej osi przyjmie postać:

[TEX]( \sqrt{x^2 + y^2}-R)^2 + z^2 = r^2,[/TEX]

co po usunięciu pierwiastka, daje równanie czwartego stopnia:

[TEX](x^2 + y^2 + z^2 +R^2 - r^2 )^2 = 4 R^2 (x^2 + y^2) .[/TEX]

• parametryczne - kartezjańskie współrzędne torusa parametryzuje się za pomocą dwóch parametrów φ i ψ, przebiegających dwa okręgi - okrąg dokonujący obrotu i okrąg, po którym porusza się środek tego pierwszego, zatem φ, ψ$\in$[0, 2π], a równania parametryczne ma postać:
  x(φ, ψ) = (R+rcosφ)cosψ,
  y(φ, ψ) = (R+rcosφ)sinψ,
  z(φ, ψ) = rsinφ.
• parametryzacja topologiczna - konstrukcja torusa przez sklejanie brzegów prostokąta może być przedstawiona jako ciągłe przekształcenie kwadratu jednostkowego (czyli iloczynu kartezjańskiego odcinków [0, 1]×[0, 1]) na iloczyn kartezjański okręgów jednostkowych O, tzn. f : [0, 1]×[0, 1] → O×O ma postać: f(s, t) = ((cos2πs, sin2πs), (cos2πt, sin2πt)).
  Z powyższej parametryzacji widać, że torus może być rozpatrywany jako podzbiór przestrzeni czterowymiarowej.

Pochodzenie nazwy:
Łacińska nazwa torusa armila oznacza pierścień żelazny używany przez wojskowych jako naramiennik. Nazwa pochodzi od słowa armus oznaczającego ramię.

Ciekawostki:
Zanim XIX wieczny matematyk francuski Yvon Villarceau [czytaj: iwą wijar'so] opisał rodzinę okręgów leżących na powierzchni torusa, zwaną dziś jego nazwiskiem, były one już wykorzystywane jako element architektoniczny i zdobniczy. Na zdjęciu poniżej przedstawiono klatkę schodową w Muzeum Katedralnym w Strasburgu pochodzącą z XVI w.

• toroid
• wielościan toroidalny
• wielościan Szilassiego
• okrąg Villarceau
• podwójny torus
• n-torus
• genus
• charakterystyka Eulera
• wstęga Möbiusa
• butelka Kleina
• rozmaitość topologiczna

Bibliografia:
Encyklopedia szkolna. Matematyka, WSiP, Warszawa 1989.