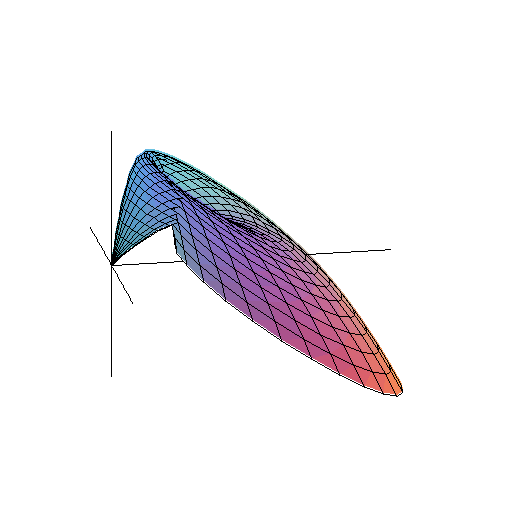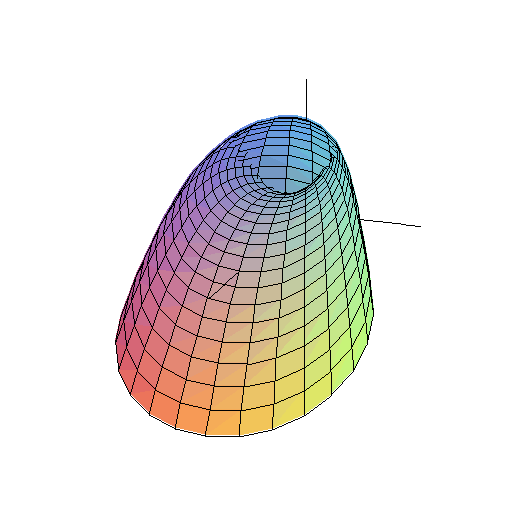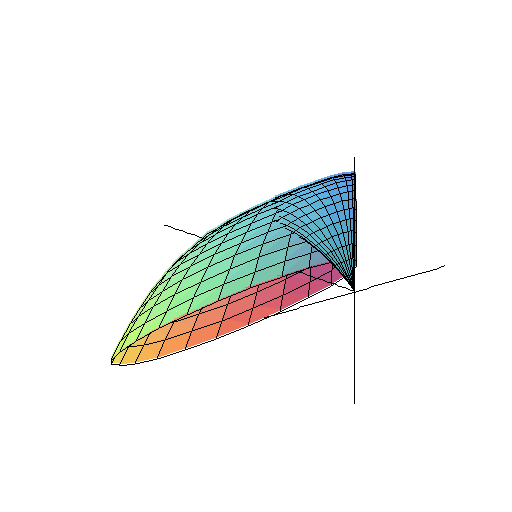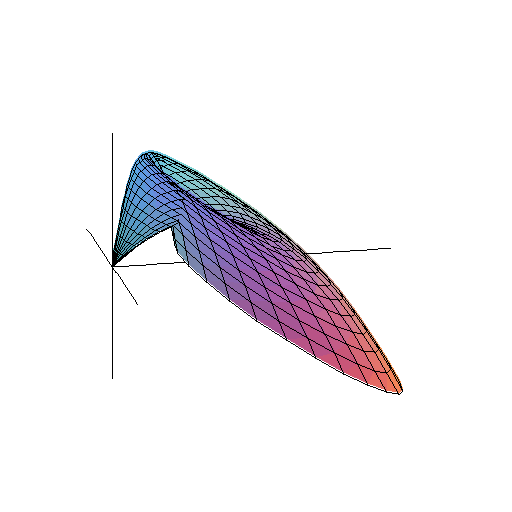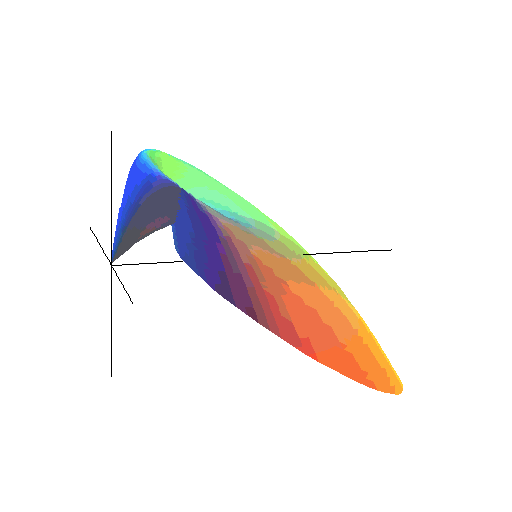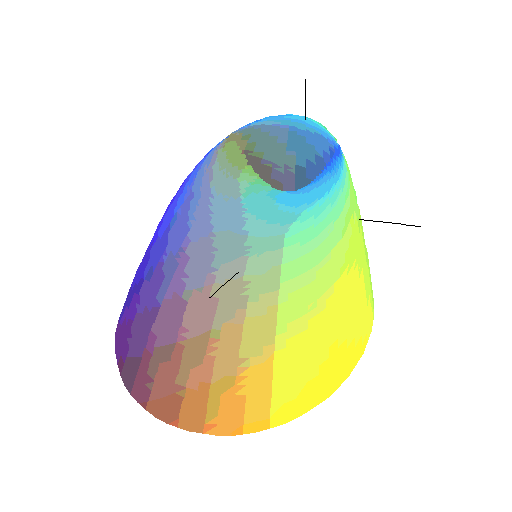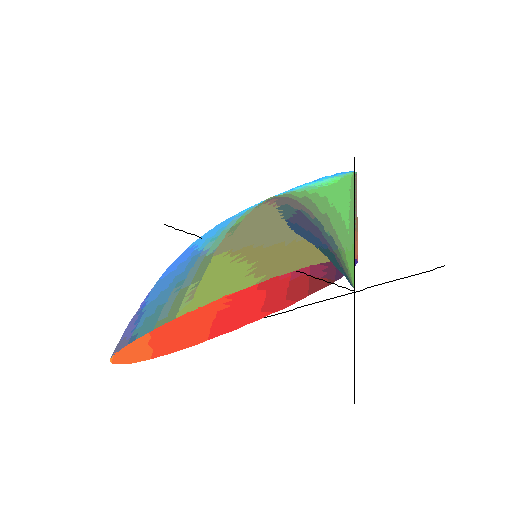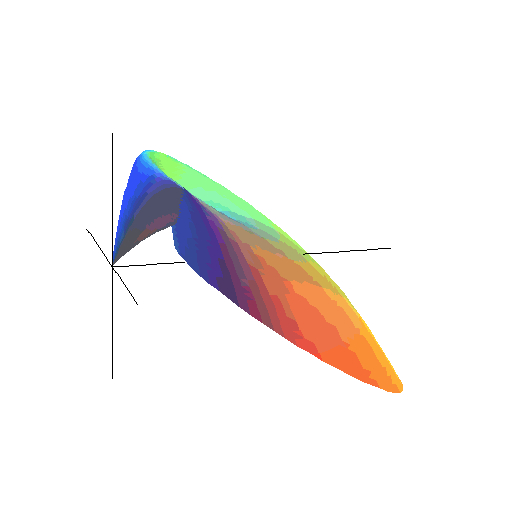Linie na tarczy

Strzelamy do celu.
Środek tarczy reprezentuje idealny strzał.
Na początek zakładamy, że pociski lecą ze stałą prędkością v, i że przy idealnym strzale pocisk leci dokładnie wzdłuż osi OX.
Gdy kierunek strzału (lufa) różni się od idealnego, to chybimy.
Chybione strzały, wystrzelone pod (ustalonym) kątem do idealnego kierunku, trafią w tarczę w punktach pewnej linii. Im będzie mniejsze, tym linia w którą trafimy, będzie bliżej celu. Zobacz.
(T oznacza czas lotu pocisku.)

Pomyślmy gdzie są wszystkie pociski wystrzelone pod ustalonym kątem (do idealnego kierunku), po T sekundach od wystrzału.
Na rysunku widać, że tworzą okrąg. Tym większy, im większe jest T.
(Środek tego okręgu nie pokrywa się z pozycją idealnego pocisku w chwili T - dlaczego?)
Wszystkie te pociski trafią w tarczę po tym samym czasie od wystrzału.
Na tarczy utworzą okrąg.

Na tarczy pokazano chybione strzały dla kątów:   ,   0,75,   0,5,   0,25.
Czy promienie okręgów na tarczy są w tej samej proporcji?

Wygląda, że tak, ale to tylko złudzenie.
(Gdyby proporcje były zachowane, to w trójkącie równobocznym dwusieczna przecinałaby wysokość w połowie, a przecież tak nie jest.)

Teraz zakładamy, że pociski lecą ze stałą prędkością v, ale przy idealnym strzale pocisk jest wystrzelony pod kątem do osi OX (leci dokładnie nad osią OX).
Tarcza jest nieco podniesiona (jak pokazano na rysunku).

Pomyślmy, gdzie są wszystkie pociski wystrzelone pod ustalonym kątem (do idealnego kierunku), po T sekundach od wystrzału.
Tak jak poprzednio utworzą okrąg. Tym większy, im większe jest T.
(By to zobaczyć, wystarczy... przekrzywić głowę.)
Jednak, odmiennie niż poprzednio, te pociski dotrą do tarczy w różnych czasach: te 'na dole' szybciej, niż te 'na górze'.
Na tarczy utworzą elipsę.

Dlaczego powstała na tarczy linia jest elipsą?
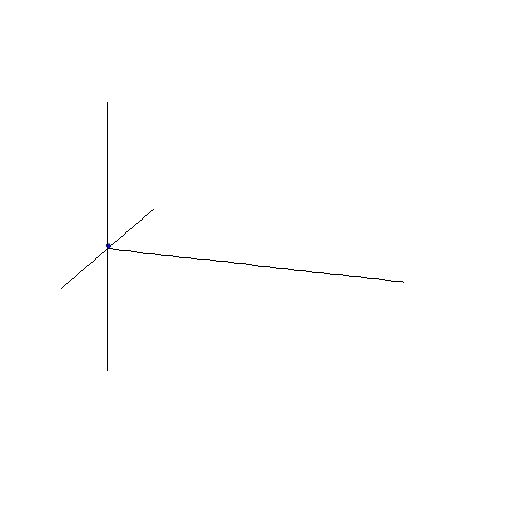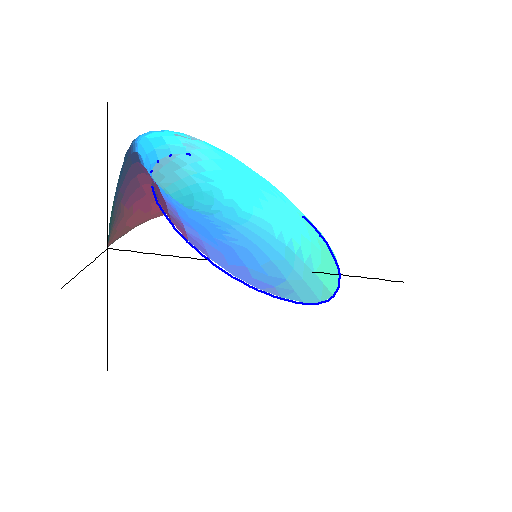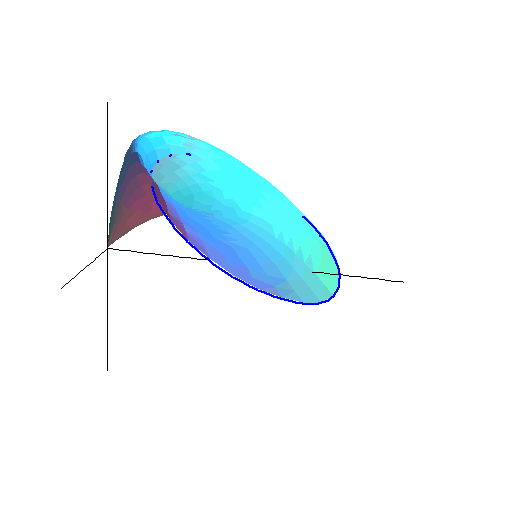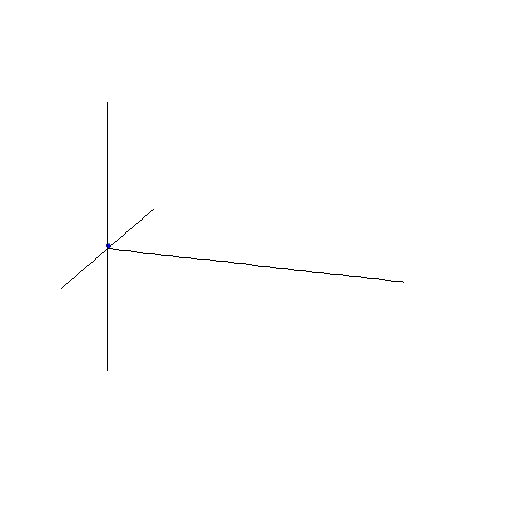
Trochę bardziej zaawansowana matematyka podpowiada, że przecinając stożek płaszczyzną, dostaniemy na powierzchni elipsę (albo hiperbolę). Tu można zobaczyć stożek - jego powierzchnię tworzą pozycje chybionych pocisków wystrzelonych pod ustalonym kątem . Ten stożek przecina płaszczyzna tarczy.

Dorzućmy do tego grawitację. Teraz dopiero zacznie się prawdziwa zabawa.

Teraz zakładamy, że pociski są wystrzeliwane ze stałą prędkością v, ale dalej oddziałuje na nie grawitacja. Na rysunku podano też wzory opisujące ruch pocisku wystrzelonego pod kątem do idealnego kierunku. Co widać?

Wydaje się, że tak jak poprzednio pociski 'lecą okręgami', to znaczy, wszystkie pociski wystrzelone pod ustalonym kątem (do idealnego kierunku), po T sekundach od wystrzału tworzą okrąg. Czy tak faktyczne jest?
Czy to można odczytać ze wzorów?
A co na to fizyka?

Zmieniaj g, zobaczysz jak leci pocisk na Księżycu, lub na Marsie.
Ponadto zmieniając g do 0, zobaczysz uzasadnienie - to faktycznie okręgi.
Czy widzisz dlaczego?

A co się dzieje z liniami na tarczy?
Eksperymentuj!

Czy umiesz tak dobrać parametry, by pocisk był wystrzelony pod (niezerowym) kątem do idealnego kierunku, a mimo to trafił do celu?
Chyba już widzisz, że linie na tarczy nie są elipsami.

Haubica, to taka armata, której cel i tarcza leżą na ziemi.
Zobacz jak wyglądają (zielone) linie na takiej tarczy.
Jakie są równania tych linii?
Czy umiesz tak dobrać parametry, by pocisk był wystrzelony pod (niezerowym) kątem do idealnego kierunku, a mimo to trafił do (zielonego) celu?

Na koniec zobaczmy, jaką powierzchnię tworzą 'lecące okręgi'.
Bez grawitacji była to powierzchnia stożka. A z grawitacją?
(Zwiększ T.)

Poniżej pokazujemy kilka rysunków tej bardzo ciekawej powierzchni.
Czy widzisz, że ma ona część zamkniętą?
(Włącz animację.)