Biznes na kempingu

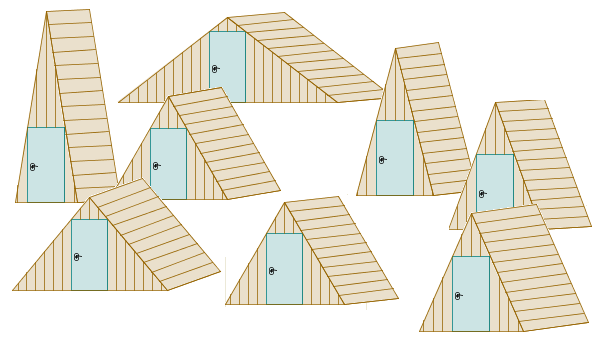
Gdzieniegdzie jeszcze (z dala od renomowanych kurortów) można napotkać takie domki kempingowe, jak powyższe. Trochę leciwe, bo z minionej epoki. Budowane bardzo oszczędnie, ledwo mieści się w nich łóżko d = 2m. Mają jednakowe drzwi a = 1m × 2m = h z nieciekawej dykty, a z tyłu okienko a = 1m × 1m = a, niewidoczne na obrazku. Widać, że były budowane seryjnie.
Zamieszkałem w jednym z nich, a w sąsiednim ulokował się znajomy, biznesmen.

 
Wiedziałem, że znajomy, prędzej czy później zada pytanie.

Kłopotliwe pytanie.   Który z domków jest najtańszy (w produkcji, nie do wynajęcia)?

Ponieważ drzwi i okna są jednakowe, domki różnią się liczbą desek użytych na dach, podłogę oraz wokół drzwi i okna. Zatem pytanie o najmniejszy koszt, jest pytaniem o najmniejsze pole powierzchni domku.

Dla rozgrzewki obliczyłem pole desek w trzech szczególnych domkach.

Zadanie 1. (na rozgrzewkę)
Jaka jest powierzchnia desek (łącznie z podłogą) w domku kempingowym, w którym:

    a)  kąt BAC = 60^o ,

    b)  kąt BAC = 45^o ,

    c)  EB = 1 .

Odpowiedzi:  
    a)  
    b)  
    c)  

Po południu zabrałem się do pracy.
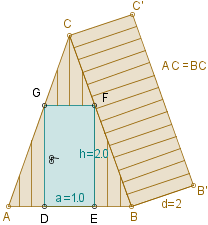
Za niewiadomą przyjąłem

Jasne jest, że dla bardzo dużych wartości x pole jest bardzo duże (większe od 4(2x+a)).
Gdy x jest bliskie 0 (ale dodatnie), to domki są bardzo wysokie i pole też jest bardzo duże.
Zatem jest czego szukać, bo dla pewnej dodatniej wartości x₀ pole jest najmniejsze.

Rachunki będą możliwe dzięki podobieństwu trójkąta ADG i połowy trójkąta GFC

skąd

Na początek znalazłem x, dla którego pole S powierzchni samego dachu jest najmniejsze.

Pole S dachu jest równe: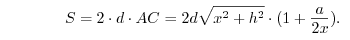

Wstawiając liczby, mamy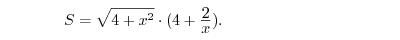

Dalej standardowo, przyrównujemy pochodną do 0.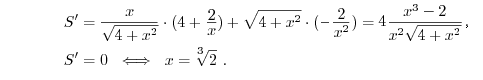

Ładny wynik! Dla takiego x pole samego dachu jest najmniejsze.
Co ciekawe, to najmniejsze pole dachu można zgrabnie zapisać:

(Zauważmy, że pierwiastek sześcienny z 2 jest liczbą niekonstruowalną, to znaczy, że za pomocą cyrkla i linijki nie można wyznaczyć tego optymalnego rozwiązania.)

Obawiam się, że powyższe dywagacje nie zainteresują sąsiada biznesmena. Jego nie interesuje piękno pierwiastków. Co więcej, powyższe rozwiązanie jest rozwiązaniem innego zagadnienia. Nie przyda się do wygrania przetargu na budowę osiedla domków kempingowych.
Zatem przejdźmy do oryginalnego problemu.

Wyznaczam pole P powierzchni wszystkich desek:

Stąd

Nie wygląda zachęcająco. Wstawiam za a, h dane liczby i obliczam, obliczam, obliczam...

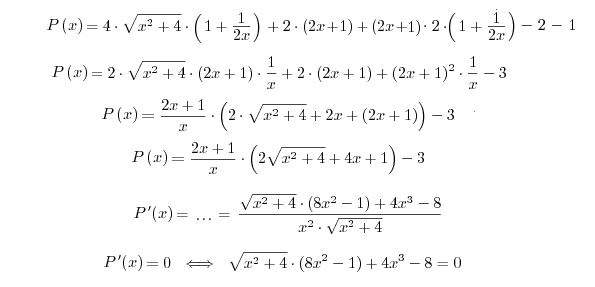
Szukane x jest pierwiastkiem ostatniego równania, które po przekształceniach (nierównoważnych) prowadzi do równania

SZÓSTEGO stopnia! Nie umiem rozwiązać tego równania.
Wiem tylko, że najmniejsza liczba desek jest dla pewnego x₀ będącego rozwiązaniem tego równania.

Wieczorem sąsiad biznesmen nie zadał mi na szczęście kłopotliwego pytania.

Nazajutrz nie dałem za wygraną.
Oznaczyłem

Ta funkcja może mieć nawet sześć miejsc zerowych. Interesują nas tylko te dodatnie.
Szacowałem:

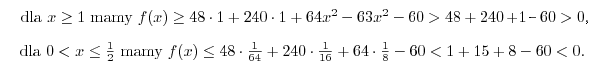
Zatem dla dodatnich argumentów funkcja f ma miejsca zerowe tylko w przedziale (0,5, 1).
Ale ile ich jest? Obliczyłem pochodną

i zauważyłem, że

Zatem w tym przedziale f jest funkcją rosnącą.
To już pewien sukces. Wiem, że dla dodatnich argumentów f ma dokładnie jedno miejsce zerowe, które leży w przedziale (0,5, 1). Zatem optymalny domek kempingowy powinien mieć szerokość pomiędzy 2,00m a 3,00m.

I tego wieczoru sąsiad biznesmen nie zadał mi kłopotliwego pytania, więc mogłem szacować dalej.

Dla dodatnich argumentów f ma dokładnie jedno miejsce zerowe, które leży w przedziale (2/3, 3/4). Zatem optymalny domek kempingowy powinien mieć szerokość pomiędzy 2,33m a 2,50m.
To już niezłe precyzja. Tylko nie wiem, jak duży błąd popełniam. Jeśli przyjmę x = 2/3, to nie wiem o ile P ( 2/3 ) różni się od optymalnego P (x₀). Wiem tylko, że x₀ jest pomiędzy 2/3 i 3/4.

Znalazłem sposób na oszacowanie tej różnicy.
Ponieważ
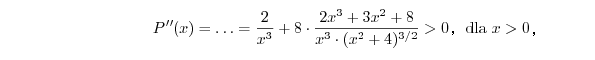
P' jest funkcją rosnącą. Ponadto

więc

Dalej z twierdzenia Lagrange'a:

stąd

Nieco lepsze oszacowanie dostaniemy dla 0,7:

Ów błąd 0,1 stanowi mniej niż 0,5% materiału potrzebnego na cały domek (bo P (0,7) > 20).
Ufff! Mam gotową odpowiedź dla sąsiada biznesmena.

Warto produkować domki o szerokości 2,40 m. Różnica pomiędzy ilością drewna na taki domek, a absolutnym minimum nie przekracza 0,1 m², to jest mniej niż 0,5% materiału potrzebnego na cały domek.

Czytelnikom, którzy dotarli do tego miejsca, zapewne spodobały się powyższe rozważania.
Takiej matematyki uczymy w szkołach (średnich i wyższych). Tylko czy...

Kłopotliwe pytanie 2.   Czy uczenie takiej matematyki to nie jest anachronizm?
Czy to nie przypomina uczenia obliczania pierwiastków kwadratowych z danych liczb, albo obsługi suwaka logarytmicznego?

Następnego dnia w ośrodku obok dorwałem się do Internetu.
Wpisałem:

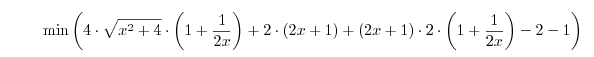
i po chwili otrzymałem:

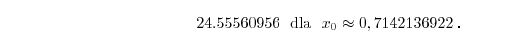
Zobaczyłem także:

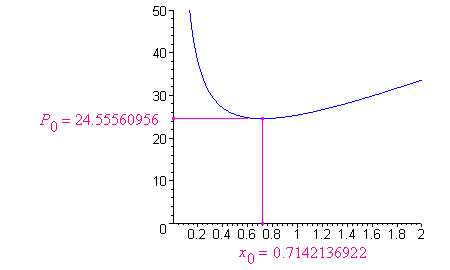
Do końca pobytu na wczasach sąsiad biznesmen nie zadał mi żadnego kłopotliwego pytania.