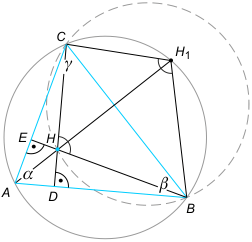
Zad. 1. Wykaż, że okręgi opisane na trójkątach ABC, ABH, BCH, ACH (gdzie H jest ortocentrum trójkąta ABC, czyli punktem przecięcia jego wysokości) są przystające.
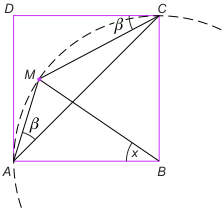
Zad. 2. Wewnątrz kwadratu ABCD obrano punkt M taki, że |∡MAC| = |∡MCD| = β. Oblicz |∡ABM|.
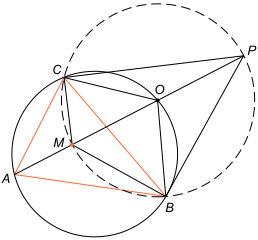
Zad. 3. Wewnątrz trójkąta ABC obrano punkt M taki, że |∡BMC| = 90° + 1/2|∡BAC| oraz że do prostej AM należy środek okręgu opisanego na trójkącie BMC. Wykaż, że M jest środkiem okręgu wpisanego w trójkąt ABC.
Zad. 4. (wolna amerykanka) W okrąg o promieniu R wpisano n-kąt foremny. Oblicz sumę kwadratów długości wszystkich jego boków i przekątnych.
W tym miesiącu maksymalną liczbę 30 punktów za zadania 1-3 otrzymują: Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Włodzimierz Bąk (nauczyciel matematyki, I LO Opole), Michel Migas (student, Politechnika Warszawska), Sabina Sy (studentka nanotechnologii, Uniwersytet Jagielloński) oraz Arkadiusz Wróbel (student, Uniwersytet Warszawski). 20 punktów zdobyła Agnieszka Borucka (uczennica, II LO Opole)
Zadanie 4 prawidłowo rozwiązali: Jacek Bagiński, Włodzimierz Bąk, Michel Migas, Tadeusz Porzucek (emeryt z Gostynia) oraz Sabina Sy.
Gratulacje.
Zadanie 1. Niech punkt H1 będzie symetryczny do ortocentrum H względem prostej BC. Wówczas |∡CH1B| = |∡CHB| = 180°-|∡HBC|-|∡HCB|= 180° - (90°-β) - (90°-γ) = β+γ. Zauważmy, że |∡CAB| + |∡CH1B| = α+β+γ = 180°. To oznacza, że punkt H1 leży na okręgu opisanym na trójkącie ABC, czyli że punkty A, B, H1 i C są współokręgowe. Ponieważ trójkąty BH1C i BHC są przystające, okręgi na nich opisane również. Zatem okrąg opisany na trójkącie BHC jest przystający do okręgu opisanego na trójkącie ABC. Dla pozostałych okręgów rozumowanie jest analogiczne.
Zadanie 2. Rozważmy okrąg opisany na trójkącie AMC. Ponieważ kąty DCM i MAC mają jednakowe miary, DC jest styczna do tego okręgu (kąty dopisany i wpisany oparte na tym samym łuku). Zatem środek okręgu opisanego na trójkącie AMC leży na przecięciu prostej CB zawierającej promień oraz symetralnej odcinka AC, a to znaczy, że leży on w punkcie B. Stąd x = 2|∡MCA| = 2(45°-β) = 90°-2β.
Zadanie 3. Niech O będzie środkiem okręgu opisanego na trójkącie BCM. Przedłużmy odcinek AM do przecięcia w punkcie P z tym okręgiem. Ponieważ |∡CMB| = 90°+α/2, mamy |∡CPB| = 90°-α/2, skąd |∡COB| = 180°-α (kąt środkowy oparty na tym samym łuku). Zatem punkt O leży na okręgu opisanym na trójkącie ABC, bo |∡CAB|+|∡COB| = α+180°-α = 180°. Zauważmy, że prosta AM jest dwusieczną kąta CAB, bo |OC|=|OB|. Z drugiej strony |∡ACB|=|∡AOB|=2|∡OPB|, bo to kąt zewnętrzny trójkąta, a to z kolei jest równe 2|∡MCB|, bo to kąt wpisany oparty na tym samym łuku MB. Oznacza to, że prosta CM jest dwusieczną kąta ACB, skąd wynika już teza.
Zadanie 4. Zaczniemy od uzasadnienia pomocniczego faktu.
Fakt. W n-kącie foremnym A1A2...An o środku O suma S wektorów OA1 + OA2+ ... + OAn = 0.
Uzasadnienie. Rozważymy dwa przypadki.
1) Jeśli n = 2k (rysunek 1), to wierzchołki Ai oraz Ai+k są symetryczne względem punktu O, więc OAi = - OAi+k. Stąd S = 0.
2) Jeśli n = 2k-1 (rysunek 2), to wierzchołki A2 i A2k-1, A3 i A2k-2 itd. są symetryczne względem prostej OA1. Oznacza to, że sumy wektorów OA2 i OA2k-1, OA3 i OA2k-2 itd. są wektorami równoległymi do wektora OA1. Możemy zatem zapisać: OA2+OA2k-1 = α2OA1, OA3 + OA2k-2 = α3OA1,..., OAk + OAk+1 = αkOA1. Stąd S = OA1 + (OA2+OA2k-1) + (OA3+OA2k-2) +....+ (OAk+OAk+1) = OA1 + (α2+α3+...+ αk)OA1 = αOA1. Analogicznie można pokazać, że S = βOA2, skąd αOA1 = βOA2. Ale wektory OA1 i OA2 nie są równoległe, co oznacza, że α = β = 0 i S = 0.
Weźmy teraz n-kąt foremny A1A2...An (rysunek 3). Rozważmy wektory A1A2, A1A3, ..., A1An. Zachodzi: A1A2 = OA2-OA1, A1A3 = OA3-OA1, ..., A1An = OAn-OA1. Wówczas A1A22 + A1A32 +...+ A1An2 = 2(n-1)R2 - 2(OA1+OA2+...+OAn-OA1)•OA1 = 2(n-1)R2 + 2OA12 = 2nR2 (korzystamy z własności iloczynu skalarnego wektorów). Ten sam wynik otrzymujemy analogicznie dla każdego z punktów A2, A3, ..., An. Dodajemy je zatem n-krotnie, a ponieważ w tej sumie długość kazdego odcinka występuje dwa razy (liczona raz z jednego, raz z drugiego wierzchołka) ostateczny wynik wynosi n·2nR2/2 = n2R2.








