Wiele szkół ma na wyposażeniu różne rodzaje klocków geometrycznych (przykładowe są opisane w dziale Pomoce naukowe, m. in. GeoMag, Reko, Zome). Klocki te można wykorzystać do samodzielnego budowania modeli przez uczniów. Problem polega na tym, że kolekcja wielościanów pojawiających się w programie nauczania szkolnego jest niewielka, a budowanie takich wielościanów z klocków jest działaniem raczej odtwórczym, rozwijającym sprawność manualną (co może mieć pewne znaczenie w przypadku młodszych uczniów), ale tylko w niewielkim stopniu rozwijającym kreatywność, pomysłowość, logiczne myślenie i wyobraźnię geometryczną.
Poniżej przedstawiamy listę zadań odkrywczych, jakie można rozwiązywać z uczniami w różnym wieku, mając do dyspozycji rozmaite klocki geometryczne. Zadania podzielono ze względu na rodzaj klocków, jakie są potrzebne do ich rozwiązania. Większość poniższych zadań nie zależy od wieku uczniów i została przetestowana na uczniach klas 4-5 SP. Wystarczy, aby uczniowie wiedzieli, jak wyglądają ostrosłupy (piramidy) i graniastosłupy (klocki). Zadania wykraczające znacznie poza poziom szkoły podstawowej zostały wyraźnie oznaczone.
Zadanie nr 2 pochodzi od prof. Michała Szurka - znanego popularyzatora matematyki, emerytowanego pracownika UW.
Zad. 1. Zbuduj wszystkie możliwe siatki:
a) czworościanu foremnego,
b) sześcianu,
c) ośmiościanu foremnego.
Sprawdź, czy wszystkie są poprawne i czy żadna się nie powtarza. Ile jest takich siatek?
Zad. 2. Zbuduj jak najwięcej wielościanów o ścianach będących trójkątami równobocznymi. Nazywamy je deltościanami (bo grecka wielka litera delta ma kształt trójkąta). Wskaż wśród nich wielościany a) foremne, b) wypukłe. Ile ich jest? Zajrzyj też do artykułu Deltościany.
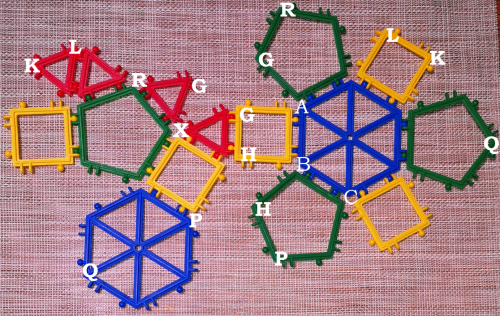
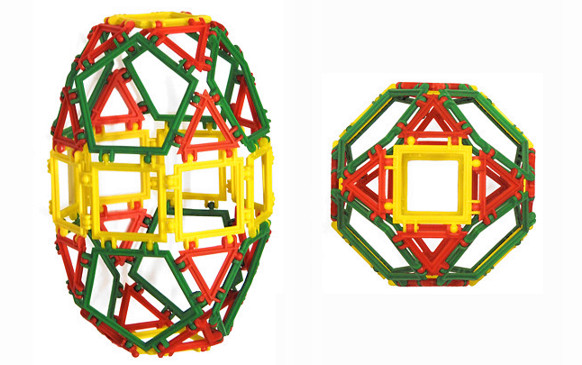
Zad. 3. a) Zbuduj jak najwięcej modeli różnych 14-ścianów. Ile z nich to wielościany wypukłe? Które z otrzymanych modeli potrafisz nazwać (zaklasyfikować do jakiejś grupy wielościanów)?

rodzina czternastościanów
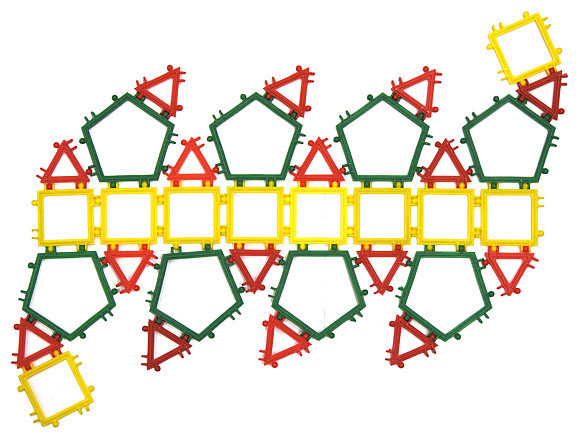
b) Zbuduj czternastościan przedstawiony na poniższych zdjęciach (a - model, b-siatka). Czy taka bryła istnieje? (LO) Uzasadnij.

Zad. 4. Zbuduj modele:
a) ostrosłupów (piramid) o różnych podstawach (foremnych i nie). Ile ścian/wierzchołków/krawędzi mają takie ostrosłupy? Których nie da się zbudować z twoich klocków? Dlaczego?


b) graniastosłupów (klocków) o różnych podstawach (foremnych i nie). Ile ścian/wierzchołków/krawędzi mają takie graniastosłupy? Których nie da się zbudować z twoich klocków? Dlaczego?
c) graniastosłupów o foremnych podstawach, w których jedna z podstaw jest przekręcona w stosunku do drugiej o połowę kąta środkowego tej podstawy (względem jej środka). W jaki sposób można połączyć te podstawy ścianami bocznymi? Jaki kształt będą miały te ściany? Takie wielościany nazywamy graniastosłupami skręconymi lub antygraniastosłupami. Ile ścian/wierzchołków/krawędzi mają takie graniastosłupy?
Zad. 5. Zbuduj modele:
a) dwupiramid o różnych podstawach (tzn. trójkątnej, kwadratowej, pięciokątnej). Dwupiramida powstaje przez sklejenie podstaw dwóch ostrosłupów o jednakowych podstawach. Jakich modeli nie możesz zbudować z twoich klocków? Dlaczego?
b) piramid przedłużonych o różnych podstawach (tzn. trójkątnej, kwadratowej, pięciokątnej). Piramida przedłużona powstaje przez przyklejenie do jednej z podstaw graniastosłupa ostrosłupa o takiej samej podstawie. Jakich
modeli nie możesz zbudować z twoich klocków? Dlaczego?
c) dwupiramid przedłużonych o różnych podstawach (tzn. trójkątnej, kwadratowej, pięciokątnej). Dwupiramida przedłużona powstaje przez przyklejenie do każdej z podstaw graniastosłupa ostrosłupa o takiej samej podstawie. Jakich modeli nie możesz zbudować z twoich klocków? Dlaczego?


d) piramid przedłużonych skręconych, w których ostrosłup przyklejany jest do podstawy odpowiedniego graniastosłupa skręconego.
e) dwupiramid przedłużonych skręconych, w których ostrosłupy przyklejane są do obu podstaw odpowiedniego graniastosłupa skręconego.
Zad. 6. Zbuduj modele:
a) kopuł, dwukopuł i klepsydr o różnych podstawach. Kopuła o podstawie wielokąta foremnego powstaje wówczas, jeśli jako ściany boczne do tej podstawy na przemian wstawimy trójkąty i kwadraty o jednakowych bokach. Jest to więc coś pośredniego między ostrosłupem (w nim jako ścian bocznych używamy tylko trójkątów) i graniastosłupem (w nim jako ścian bocznych używamy tylko kwadratów/prostokątów). Sczepiamy sąsiednie ściany boczne, a powstającą dziurę na górną podstawę kopuły zaklejamy odpowiednim wielokątem. Jakie wielokąty mogą stanowić dolną podstawę kopuły? A jakie górną? Dwukopuła to dwie jednakowe kopuły sklejone dolnymi podstawami. Klepsydra to dwie jednakowe kopuły sklejone górnymi podstawami. Dwukopuła może być dwóch rodzajów: prosta - jeśli sklejając kopuły podstawami, przyłożymy trójkąty do trójkątów i kwadraty do kwadratów, lub przekręcona - jeśli trójkąty przyłożmy do kwadratów. Klepsydra również może być prosta lub przekręcona. Wykonaj odpowiednie modele.

b) kopuł, dwukopuł i klepsydr przedłużonych o różnych podstawach.
c) kopuł, dwukopuł i klepsydr przedłużonych skręconych o różnych podstawach.
d) kopułopiramid i klepsydropiramid o różnych podstawach.
Co to za wielościany? Których z nich nie da się wykonać z twoich klocków? Dlaczego?
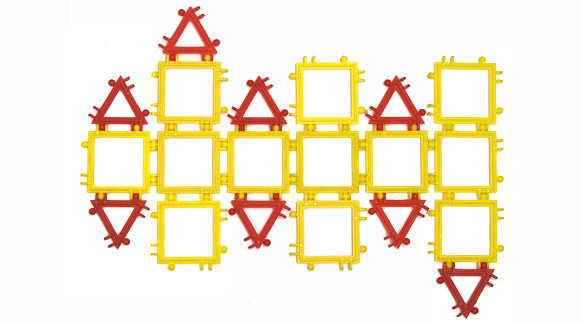


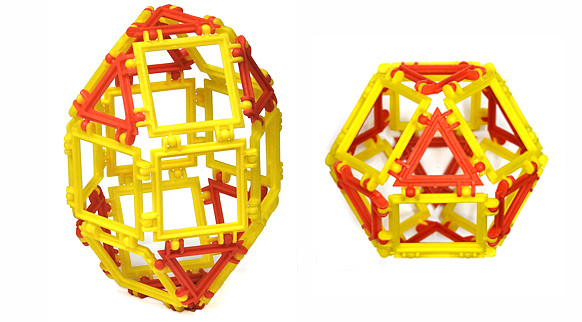
Zad. 7. Zbuduj modele:
a) rotund, dwurotund i hantli o różnych podstawach. Rotunda o podstawie wielokąta foremnego powstaje wówczas, jeśli jako ściany boczne do tej podstawy na przemian wstawimy trójkąty i pięciokąty foremne o jednakowych bokach. Sczepiamy sąsiednie ściany boczne, a powstającą gwiaździstą dziurę zaklejamy odpowiednim wielokątem w górnej podstawie z doczepionymi trójkątami równobocznymi na bokach, co zamyka całą bryłę. Jakie wielokąty mogą stanowić dolną podstawę rotundy? A jakie górną? Dwurotunda to dwie jednakowe rotundy sklejone dolnymi podstawami. Hantle to dwie jednakowe rotundy sklejone górnymi podstawami. Dwurotunda może być dwóch rodzajów: prosta - jeśli sklejając rotundy podstawami, przyłożymy trójkąty do trójkątów i pięciokąty do pięciokątów, lub przekręcona - jeśli trójkąty przyłożmy do pięciokątów. Hantle również mogą być proste lub przekręcone. Wykonaj odpowiednie modele.

b) rotund, dwurotund i hantli przedłużonych o różnych podstawach.
c) rotund, dwurotund i hantli przedłużonych skręconych o różnych podstawach.
d) kopułorotund i piramidorotund o różnych podstawach.
e) kopułohantli i piramidohantli o różnych podstawach.
Co to za wielościany? Których z nich nie da się wykonać z twoich klocków? Dlaczego?

Zad. 8. Zbuduj modele:
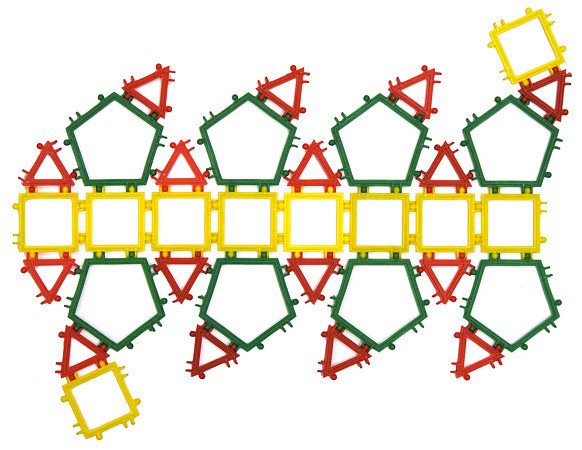
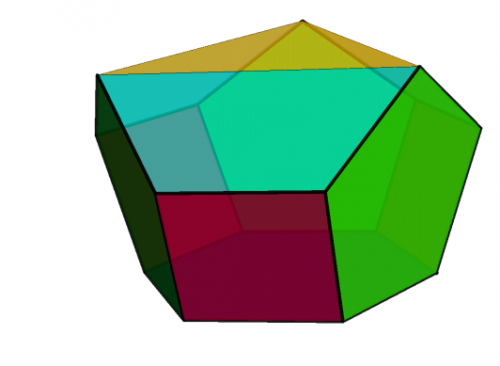
a) koron o różnych podstawach. Korona o podstawie wielokąta foremnego powstaje wówczas, jeśli jako ściany boczne do tej podstawy na przemian wstawimy kwadraty i pięciokąty foremne o jednakowych bokach. Sczepiamy sąsiednie ściany boczne, a pozostałą dziurę zaklejamy... No własnie, czym?
Rysunki poniżej przedstawiają koronę sześciokątną (tzn. jej dolna podstawa jest sześciokątem foremnym, a górna - trójkątem równobocznym) i jej siatkę. Całość zamykają trapezy złożone z trzech trójkątów równobocznych.

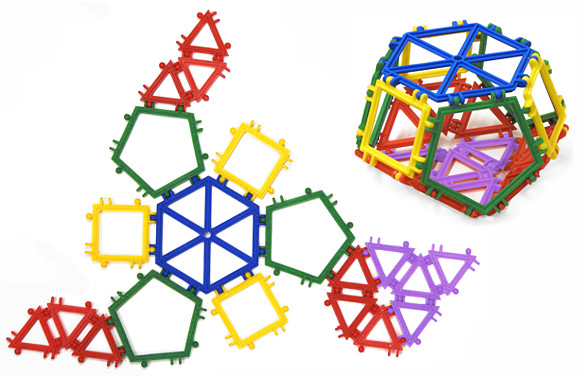
b) dwukoron o różnych podstawach, prostych i przekręconych, a także dwukoron przedłużonych i przedłużonych skręconych.
c) dwóch koron sklejonych górnymi podstawami. Jak nazwałbyś takie wielościany?
d) piramidokoron, kopułokoron, rotundokoron, itd.
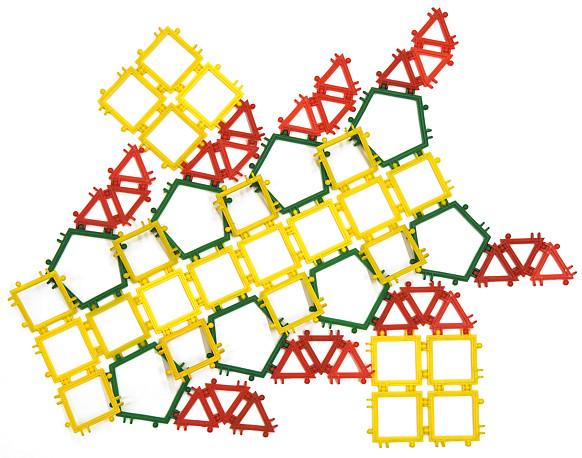
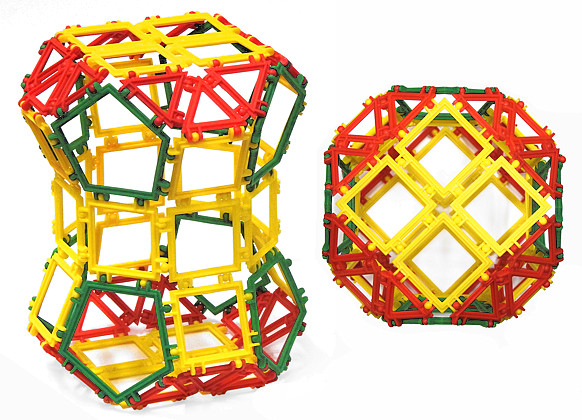
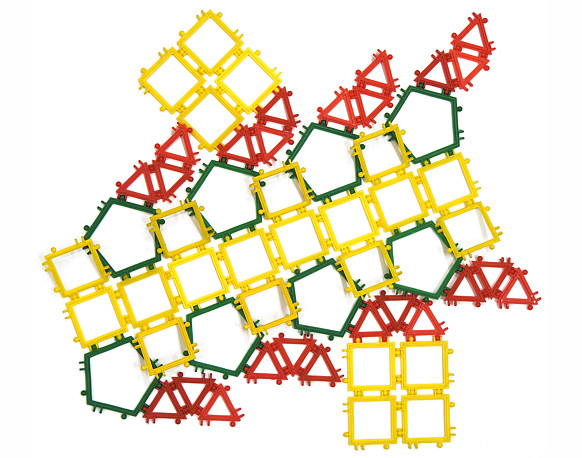
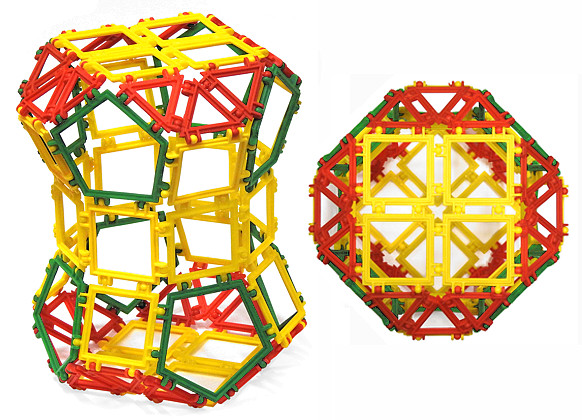
Zad. 9. Iluścianem jest korona szesciokątna? Zmodyfikuj ten wielościan, aby otrzymać kolejny przykład czternastościanu z zad. 2.
Zad. 10. Zbuduj model "całujących się kermitów". Bryła ta składa się z dwóch dwupiramid pięciokątnych o prostopadłych osiach sklejonych czterema krawędziami bocznymi (rys. poniżej). (LO) Jest to przykład bryły bistabilnej. Dowiedz się na czym polega ta własność. Zbuduj modele innych takich brył. Zaobserwuj własność bistabilności, wykonując też modele z papieru.
rys
Zad. 11. Zbuduj modele:
a) sześcianu z dobudowanymi piramidami zamiast każdej ze ścian. Ile z tych piramid można dobudować do wewnątrz? Ile ścian ma otrzymany wielościan? Co to za wielościan? Od czego to zależy?
b) czworościanu foremnego z dobudowanymi czworościanami foremnymi zamiast każdej ze ścian. Ile ścian ma otrzymany wielościan? Co to za wielościan? W jaki inny sposób mogła powstać ta bryła?
c) różnych graniastosłupów powiększonych, tzn. takich, które na jednej lub kilku ścianach bocznych mają dobudowane piramidy (w zależności od liczby ścian zastąpionych piramidami, mówimy o graniastosłupie powiększonym jednokrotnie, dwukrotnie itd).
d) ciekawych stożkowań innych wielościanów (ze stożkowaniem wielościanu mamy do czynienia wtedy, gdy na każdej z jego ścian jako na podstawie wybudujemy ostrosłup).
Zad. 12. Zbuduj modele wszystkich wielościanów platońskich. Ile ich jest? Ile ścian/wierzchołków/krawędzi mają te wielościany? Które z otrzymanych modeli potrafisz zaklasyfikować do jakiejś grupy wielościanów? (LO) Skąd wiadomo, że to są wszystkie wielościany platońskie?
Zad. 13. Zbuduj modele wszystkich wielościanów platońskich ściętych (znikają krawędzie) i przyciętych (krawędzie nie znikają i są przycięte w taki sposób, żeby nowo powstające ściany były foremne).
Zad. 14. Wyobraź sobie, że w każdym z wielościanów platońskich na środku każdej ściany obieramy punkt i łączymy krawędziami te punkty, które leżą na sąsiednich ścianach. Jakie wielościany otrzymamy? Nazywamy je dualnymi do tych, z których powstały. Zbuduj kilka innych modeli wielościanów. Spróbuj naszkicować ich wielościany dualne. Jak wyglądają wielościany dualne do a) ostrosłupów, b) graniastosłupów, c) graniastosłupów skręconych? (LO) Jak wyglądają wielościany dualne do wielościanów dualnych? Co to są wielościany samodualne? Podaj przykłady takich wielościanów.
Zad. 15. (LO) Zbadaj zależności między różnymi siatkami (z zad. 2):
a) czworościanu foremnego i jego dualnej kopii,
b) sześcianu i dualnego do niego ośmiościanu foremnego. Opracuj metodę znajdowania wszystkich możliwych siatek ośmiościanu foremnego na podstawie znajomości 11 siatek sześcianu.
Zad. 16. Zbuduj modele:
a) piłki nożnej
b) wielościanów wypukłych o foremnych ścianach i jednakowych wszystkich narożach. Takie wielościany nazywamy archimedesowymi. Ile jest takich wielościanów? Które z otrzymanych modeli potrafisz nazwać (zaklasyfikować do jakiejś grupy wielościanów)? (LO) Skąd wiadomo, że innych wielościanów archimedesowych nie ma?
c) kilku wielościanów wypukłych o foremnych ścianach, ale nieprzystających narożach. Takie wielościany nazywamy johnsonowskimi. Które z otrzymanych modeli potrafisz nazwać (zaklasyfikować do jakiejś grupy wielościanów)? Ile jest wielościanów johnsonowskich?
Zad. 17. (LO) Jak wyglądają wielościany dualne do różnych wielościanów:
a) archimedesowych?
b) johnsonowskich?
Zad. 1. Zbudu model układu współrzędnych kartezjańskich:
a) na płaszczyźnie z zaznaczonym punktem w ustalonej ćwiartce i jego współrzednymi na osiach,
b) w przestrzeni z zaznaczonym punktem w ustalonym oktancie i jego współrzędnymi na osiach.
Zad. 2. Zbuduj model równobocznego krzyża:
a) płaskiego o 4 ramionach parami prostopadłych, powstającego z przecięcia dwóch przystających prostokątów,
b) przestrzennego o 6 ramionach parami prostopadłych, powstającego z przecięcia trzech przystających prostopadłościanów.
Zad. 3. Zbuduj model przestrzenny drukowanej litery T. Dobierz właściwe proporcje wymiarów.







