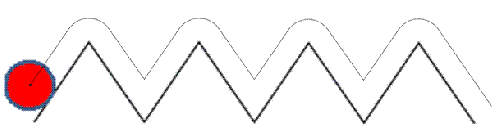
Zad. 1. Jaki tor wykreśli środek koła toczącego się po drodze o takim profilu?
Zad. 2. Na stole leży 2018 patyczków. Dwie osoby grają w Patyczaka: zabierają na przemian ze stołu 1, 2, 3, ..., 9, 10 lub 11 patyczków. Wygrywa ten, kto weźmie ostatni patyczek. Czy któryś z graczy ma strategię wygrywającą? Jeśli tak, to który i na czym polega jego strategia?
Zad. 3. Kwadratową kartkę papieru zaginano n razy w taki sposób, aby kolejne zagięcia dzieliły kartkę na możliwie największą liczbę wielokątów. Ile wynosi ta liczba dla n = 3, 4, 5? Podaj wzór funkcji przedstawiającej zależność liczby powstałych wielokątów od liczby wykonanych zagięć.
W maju punkty zdobyli:
- 3 pkt. - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr, Krzysztof Danielak - student informatyki przemysłowej na PWr,
- 2 pkt. - Piotr Mazur - urzędnik ze Złotoryi,
- 1 pkt. - Krystyna Lisiowska - redaktor z Warszawy.
Za pozostałe odpowiedzi nie przyznano punktów.
Po ośmiu miesiącach Ligi w czołówce znajdują się:
- 21,25 pkt. - Piotr Mazur,
- 19,5 pkt. - Krystyna Lisiowska,
- 19,25 pkt. - Małgorzata Konarska.
Zad. 1. Zadanie pochodzi z konkursu Kangur Matematyczny 2017. Odpowiedź przedstawia rysunek. Ruch środka koła można prześledzić, oglądając ten film.
Zad. 2. Jest to przykład znanej gry NIM. Żeby mieć pewną wygraną, trzeba przed swoim ostatnim ruchem zastać na stole 1, 2, 3, ... lub 11 patyczków. Aby zmusić przeciwnika do wytworzenia takiej sytuacji, w przedostatnim swoim ruchu trzeba pozostawić na stole 12 patyczków. Analogicznie, żeby dało się to zrobić, musimy przed tym ruchem zastać na stole 13, 14, 15, ... lub 23 patyczki, co z kolei możemy sobie zapewnić przez pozostawienie w poprzednim ruchu na stole 24 patyczków. Powtarzając to rozumowanie (dodając 12), dojdziemy do wniosku, że aby zapewnić sobie wygraną, musimy w pewnym ruchu zostawić na stole 2016 patyczków. Jest to możliwe, jeśli zaczynamy grę. Strategię wygrywającą ma więc gracz rozpoczynający.
Zad. 3. W celu zmaksymalizowania liczby wielokątów żadne proste zagięć nie mogą być równoległe, każda musi się przecinać z każą inną wewnątrz kartki i w żadnym punkcie przecięcia nie mogą schodzić się trzy proste. Wówczas otrzymujemy dla 3 prostych 7 wielokątów, dla 4 - 11, a dla 5 - 16. Dla n zagięć liczba wielokątów wynosi f(n) = 1/2n(n+1)+1. Uzasadnić można ten wzór rekurencyjnie. Jedna prosta dzieli kartkę na 2 części. Jeśli n prostych dzieli kartkę na f(n) części, to poprowadzenie kolejnej prostej dorzuca nowych n+1 wielokątów, ponieważ każda prostabiegnąc do punktu przecięcia przedziela jakiś istniejący już wielokąt na dwa, punktów przecięcia jest n (bo z każdą prostą jest inny) oraz za ostatnim punktem przecięcia dodana prosta rozcina jeszcze jeden obszar. Mamy zatem f(1)=2, f(n+1) = f(n)+n+1. To daje ciąg sum początkowych liczb naturalnych powiekszonych o 1.







