W poprzednim odcinku ligi postawiliśmy następujący problem: jeśli wiemy, że tramwaj, którym chce podróżować pasażer, kursuje co 20 minut, to jakie jest prawdopodobieństwo, że tramwaj nadjedzie w ciągu najbliższych 5 minut na przystanek, na którym pasażer ów oczekuje? Rozwiązaniem tego zadania jest liczba 5/20 = 1/4. Moglibyśmy ten sam problem postawić nieco bardziej ogólnie, modyfikując nieznacznie przykład sprzed miesiąca.
Przykład 1. Podróżny przybywa na przystanek tramwajowy. Nie ma świadomości, która jest godzina. Wie, że na tym przystanku zatrzymują się tramwaje tylko jednej linii i że kursują one co 20 minut, jednak nie wie, jak dawno temu ostatni raz przejeżdżał tramwaj. Jakie jest prawdopodobieństwo, że jeśli nie wystąpią żadne nieprzewidziane okoliczności, kolejny tramwaj nadjedzie w ciągu najbliższych t minut? Rozważ wszystkie rzeczywiste wartości t.
Rozwiązanie. Jest oczywiste, że jeśli weźmiemy t<0, to rozważane prawdopodobieństwo, że w ciągu t minut nadjedzie tramwaj, będzie wynosiło 0 (nie zakładamy możliwości podróży w czasie). Jeśli weźmiemy t>20, to jest z kolei oczywiste, że rozważane prawdopodobieństwo wynosi 1 (bo skoro tramwaje kursują co 20 minut, to w ciągu najbliższych ponad 20 minut tramwaj musi przjechać). Pozostaje zatem rozważenie $t\in [0,20]$. Wszystkie możliwe momenty przybycia tramwaju obrazuje przedział [0,20], z czego interesują nas momenty przybycia tramwaju do chwili t czyli przedział [0,t]. W takim razie rozważane prawdopodobieństwo jest równe ilorazowi długości tych przedziałów czyli t-0/20-0=t/20.
W ten sposób otrzymaliśmy funkcję, którą można opisać wzorem:
$F(t)=\left\{\begin{array}{c,l}0,& t<0\\ \frac{t}{20},& t\in[0,20]\\ 1,& t>20\end{array}.\right.$
Poniżej można obejrzeć jej wykres (proporcje jednostek na osiach celowo zostały zaburzone):

Przykład posłużył nam do ilustracji bardzo ważnego obiektu w rachunku prawdopodobieństwa. Obiektem tym jest dystrybuanta. Zanim jednak przedstawimy definicję dystrybuanty, musimy poznać jeszcze jedno pojęcie.
W naszych dalszych rozważaniach przewijać się będzie pojęcie zmiennej losowej. Cóż to takiego? Najkrócej i nieformalnie można by powiedzieć, że zmienna losowa to wielkość liczbowa, której dokładna wartość zależy od losowych okoliczności. Dla przykładu: średnica pięciozłotówki nie jest dobrym przykładem zmiennej losowej, ponieważ jest ona ściśle określona. Jednak średnica kropli wody kapiącej z kranu może być potraktowana jako zmienna losowa. Liczba płotków ustawiona na bieżni w czasie biegu na ustalonym dystansie nie jest dobrym przykładem zmiennej losowej, jednak liczba płotków, jakich zawodnik nie przewrócił w czasie biegu, jak najbardziej może być potraktowana jako zmienna losowa. Zmienną losową może być liczba oczek wyrzucona na kostce do gry. Może nią być także czas oczekiwania na tramwaj w powyższym przykładzie.
Zmiennej losowej jako takiej nie można obserwować. Można za to obserwować jej różne wartości (zwane też realizacjami). Nie ma czegoś takiego jak średnica kropli wody jako taka. Można za to mierzyć średnice poszczególnych kropel. Nie jest nigdzie powiedziane, ile płotków zawodnik pokona bez ich przewrócenia, można jednak badać, ile płotków nie zostało wywróconych przez poszczególnych zawodników. Można obserwować, ile oczek wypadło na kostce w poszczególnych rzutach. Można też badać, jak długo od przybycia na przystanek poszczególni pasażerowie oczekują na tramwaj, natomiast wiadomo, że czas ten może być zupełnie różny nawet dla różnych przejazdów tego samego pasażera, o ile w planowaniu godziny przybycia na przystanek nie kieruje on się rozkładem jazdy.
Dystrybuantą zmiennej losowej X nazywamy funkcję zadaną wzorem F(t) = P(X≤t), określoną dla każdej liczby rzeczywistej t.
Funkcja, którą otrzymaliśmy w przykładzie 1, to właśnie dystrybuanta. Tak się składa, że tamta konkretna dystrybuanta jest funkcją ciągłą (tzn. taką, że jej wykres można narysować bez odrywania ołówka od kartki), ale tak nie musi być zawsze. Jeśli zmienna losowa, której dystrybuantę rozważamy, może przyjmować tylko skończoną liczbę wartości (np. sześć możliwych wyników w rzucie jedną kostką do gry), to dystrybuanta takiej zmiennej losowej nie będzie ciągła.
Przykład 2. Rozważamy rzut symetryczną monetą tzn. taką, że prawdopodobieństwa wyrzucenia orła i reszki są takie same i wynoszą ½. Gra toczy się o jednogroszówkę znalezioną na ulicy przez Adama i Bartka; ponieważ obaj zauważyli ją jednocześnie i nie da jej się już rozmienić, postanowili, że rzucą monetą i ten, kto dobrze obstawi wynik rzutu, wygra jednogroszówkę. Adam obstawił orła a Bartek reszkę. Niech zmienna losowa X oznacza wielkość wygranej Bartka (w gr) w tej grze. Wyznacz dystrybuantę zmiennej losowej X.
Rozwiązanie. Aby wyznaczyć dystrybuantę zmiennej losowej X, podzielimy zbiór liczb rzeczywistych na trzy przedziały i będziemy rozważać $t \in (-\infty, 0)$, $t \in [0, 1)$ i $t \in [1,\infty)$.
Jeśli weźmiemy $t \in (-\infty, 0)$, to wówczas $P(X \leq t) =0$, bo X nie może przyjmować żadnej ujemnej wartości.
Jeśli $t \in [0, 1)$, to $P(X \leq t)=P(X=0)=\frac{1}{2}$.
Jeśli z kolei $t \in [1,\infty)$, to $P(X \leq t)=P(X=0 \ lub \ X=1)=1$, bo 0 i 1 to jedyne wartości, jakie może przyjmować X
Wobec tego możemy napisać:
$F(t)=\left\{\begin{array}{c,l}0,& t<0\\ \frac{1}{2},& t\in[0,1)\\ 1,& t\geq 1\end{array}.\right.$
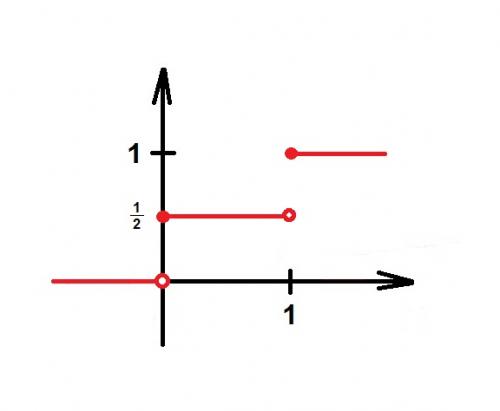
Zwróćmy uwagę, że jeśli dystrybuanta jest funkcją ciągłą, to aby obliczyć, jakie jest prawdopodobieństwo, że zmienna losowa znajduje się w jakimś przedziale, wystarczy obliczyć różnicę dystrybuanty na końcach tego przedziału
Przykład 3. Wróćmy do przykładu z oczekiwaniem na tramwaj. Nietrudno zauważyć, że prawdopodobieństwo tego, że czas oczekiwania na tramwaj mieści się w przedziale [5 min,10 min] (przy czym równie dobrze mógłby być to przedział otwarty), wynosi ¼. Jednocześnie
$P(X\in [5,10])=F(10)-F(5)=\frac{10}{20}-\frac{5}{20}=\frac{5}{20}=\frac{1}{4}$.
Prawdopodobieństwo tego, że zmienna losowa znajdzie się w ustalonym przedziale, często można wyrazić także za pomocą innej funkcji niż dystrybuanta. Jeśli istnieje funkcja f określona na całym zbiorze liczb rzeczywistych, o wartościach nieujemnych, taka że dla dowolnych liczb a i b takich że a≤b (przy czym może się zdarzyć, że a = -∞ lub b = ∞) liczba $P(X\in[a,b])$ jest równa polu pod wykresem funkcji f nad przedziałem [a,b], to funkcję f nazywamy gęstością zmiennej losowej X.
Powróćmy do przykładu z tramwajem.
Przykład 4. Nietrudno zauważyć, że jeśli $a, b \in [0,20]$ i $a\leq b$, to $P(X\in[a,b])=\frac{b-a}{20}$ (można się o tym przekonać np. opierając się na dystrybuancie podobnie jak w przykładzie 3). W takim razie gęstość zmiennej losowej X będzie miała postać:
$f(t)=\left\{\begin{array}{c,l} \frac{1}{20},& t\in[0,20]\\ 0,& t\in (-\infty,0)\cup(20,\infty) \end{array}.\right.$
gdyż jeśli $a, b \in [0,20]$ i $a\leq b$, to pole pod wykresem tej funkcji nad przedziałem $[a,b]$ wynosi właśnie $(b-a) \cdot \frac{1}{20} = \frac{b-a}{20}$. Zwróćmy uwagę, że to, jak będzie określona gęstość w punktach 0 i 20, nie ma znaczenia. Można tam położyć zarówno 0 jak i 1/20.
Na poniższym wykresie ukazującym gęstość opisaną powyżej, proporcje jednostek na poszczególnych osiach zostały celowo zaburzone, by zwiększyć czytelność wykresu.

Przykład 5. Mając daną gęstość, możemy na jej podstawie skonstruować dystrybuantę. Wystarczy dla każdej liczby t obliczyć pole pod wykresem gęstości nad przedziałem $(-\infty,t)$. Jeśli gęstość jest zadana jak w przykładzie 4, to nietrudno jest zauważyć, że
- jeśli t<0, to pole pod wykresem gęstości nad przedziałem $(-\infty,t)$ wynosi 0, bo i sama gęstość jest tam równa 0,
- jeśli $t\in[0,20]$, to obszar pod wykresem gęstości nad tym przedziałem jest w istocie prostokątem o bokach długości t i 1/20, a zatem jego pole wynosi t · 1/20 = t/20,
- jeśli t>20, to obszar pod wykresem gęstości nad tym przedziałem jest w istocie prostokątem o bokach długości 20 i 1/20, a zatem jego pole wynosi 20 · 1/20 = 1.
Łącząc trzy powyższe przypadki we wzór funkcji, otrzymamy dystrybuantę jak w przykładzie 1.
Gęstość oddaje następującą intuicję: gęstość jest duża w obszarze tych wartości, które zmienna losowa często przyjmuje, i mała w obszarach, gdzie zmienna losowa rzadko przyjmuje jakąś wartość. Gdybyśmy np. zastanawiali się, jak może wyglądać gęstość zmiennej losowej oznaczającej Odległość, jaką uzyskują zawodnicy w pchnięciu kulą (w metrach), to jej wykres mógłby wyglądać podobnie jak ten:

Wykres gęstości tej zmiennej losowej można by zinterpretować w następujący sposób: wielu zawodników uzyskuje wyniki przeciętne, od czasu do czasu komuś zdarza się zupełnie zepsuć rzut i uzyskać bardzo słaby rezultat, a od czasu do czasu bije się rekordy.
Na koniec jeszcze jedna ważna uwaga. Warto, aby czytelnik poświęcił nieco czasu na jej przemyślenie. Nie każda zmienna losowa ma gęstość, ale każda ma dystrybuantę. W szczególności gęstości nie mają zmienne losowe, które przyjmują tylko skończenie wiele wartości, tak jak zmienna losowa związana z rzutem monetą, którą rozważaliśmy w przykładzie 2. To samo można wyrazić, mówiąc, że jeśli dystrybuanta danej zmiennej losowej ma "skoki" (nie jest ciągła), to ta zmienna losowa nie ma gęstości.
[koniec wykładu dla gimnazjalistów]
Wspomnieliśmy powyżej o związku, jaki łączy gęstość (jeśli istnieje) z dystrybuantą. Przedstawiliśmy jednak ten związek dość nieformalnie, w języku pola pod wykresem gęstości. W miarę nauki matematyki i poznania rachunku różniczkowego i całkowego dowiecie się (w szkole lub na studiach, jeśli w ich trakcie będziecie się uczyli matematyki), jaki jest związek między gęstością i dystrybuantą. Już teraz możemy, decydując się na niewielkie uproszczenie, napisać tu, że gęstość jest pochodną dystrybuanty, a dystrybuanta funkcją pierwotną gęstości.
Zadanie 1. Wykres przedstawia gęstość pewnej zmiennej losowej.
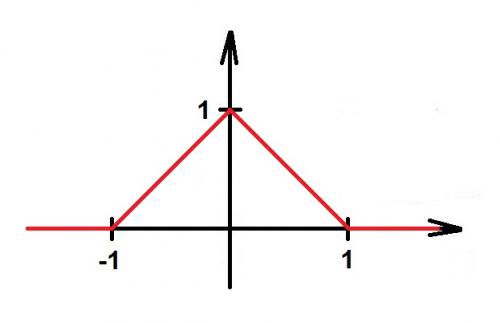
Wyznacz wzorem jej dystrybuantę.
Zadanie 2. Dystrybuanta pewnej zmiennej losowej X zadana jest wzorem:
$F(x)=\left\{\begin{array}{cl} 0,& t<0 \\ 1-\frac{1}{(t+1)^2}, & t\geq 0\end{array}.\right.$
Znajdź takie $c$, że $P(X>c)=1-P(X\leq c)<0,000001$.
Zadanie 3. Rzucamy jeden raz kostką do gry w postaci czworościanu foremnego (bryły o czterech ścianach, z których każda je trójkątem równobocznym; na każdej ze ścian jest liczba od 1 do 4). Niech X będzie wynikiem takiego rzutu tzn. liczbą wypisaną na ściance, na której kostka leży. Wyznacz wzorem dystrybuantę zmiennej losowej X.
Zadanie 1. Dystrybuanta pewnej zmiennej losowej X zadana jest wzorem:
$F(x)=\left\{\begin{array}{cl} 0,& t<0 \\ 1-\left(\frac{1}{2}\right)^x, & t\geq 0\end{array}.\right.$
Oblicz prawdopodobieństwo, że $X\in [1,2]\cup[3,4]\cup[5,6]\cup\dots$.
Wskazówka: jeśli $|q|<1$, to $1+q+q^2+q^3+\dots=\frac{1}{1-q}$.
Zadanie 2. Uzasadnij, że funkcja postaci
$f(x)=\left\{\begin{array}{cl} 0,& t\in(-\infty,0)\cup(4,\infty) \\ 2-\frac{1}{2}x, & t\in[0,4]\end{array}\right.$
nie jest gęstością żadnej zmiennej losowej.
Zadanie 3. Rzucamy sześcienną kostką do gry. Niech X oznacza resztę z dzielenia liczby uzyskanych oczek przez 4. Wyznacz wzorem dystrybuantę zmiennej losowej X.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Joanna Lisiowska | 0 | 1 | 0 | 1 |
| Adam Stachelek | 1 | 0,5 | 1 | 2,5 |
Klasyfikacja generalna:
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 5 punktów
Joanna Lisiowska (Katolicki Zespół Edukacyjny im. Piotr Skargi w Warszawie) - 4 punkty
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 2 punkty
Dawid Konieczko (Społeczne Gimnazjum z Oddziałami Dwujęzycznymi w Szprotawie) - 0 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Daria Bumażnik | 1 | 0 | 1 | 2 |
| Tomasz Stempniak | 1 | 0 | 1 | 2 |
Klasyfikacja generalna:
Tomasz Stempniak (I Liceum Ogólnokształcące w Ostrowie Wielkopolskim ) - 5 punkty
Daria Bumażnik (II Liceum Ogólnokształcące im. C. K. Norwida w Jeleniej Górze) - 3 punkt
Witold Barcz (Zespół Szkół Elektryczno-Mechanicznych w Nowym Sączu) - 1 punkt
Zad. 1. Ponieważ dystrybuanta w punkcie t jest równa polu pod wykresem gęstości nad przedziałem (-∞,t], więc widzimy, że
- jeśli t < -1, to pole to jest równe 0,
- jeśli t∈[-1,0), to pole to jest równe polu równoramiennego trójkąta prostokątkego o przyprostokątnej długości t-(-1) = t+1, czyli jest równe ½(t+1)2,
- jeśli t∈[0,1), to pole to jest równe sumie pól równoramiennego trójkąta prostokątkego o przyprostokątnej długości 1 i trapezu prostokątnego o podstawach dugości 1 i 1-t i wysokości t, czyli jest równe ½·12+½·(1+(1-t))·t = ½+½·(2-t)·t = ½(1+2t-t2),
- jeśli t ≥ 1, to pole to jest równe polu równoramiennego trójkąta prostokątnego o przyprostokątnej długości √2, czyli jest równe ½·(√2)2=1.

W takim razie
$F(x)=\left\{\begin{array}{cl} 0, & t<0 \\ \frac{1}{2}(t+1)^2, & t\in [-1,0) \\ \frac{1}{2}(1+2t-t^2),& t\in[0,1) \\ 1,& t\geq 1 \end{array}\right. .$
Zad. 2. Zgodnie z definicją dystrybuanty jeśli c > 0, to
$P(X>c)=1-P(X\leq c)=1-\left[1-\frac{1}{(c+1)^2}\right]=1-1+\frac{1}{(c+1)^2}=\frac{1}{(c+1)^2}.$
Rozwiązujemy nierówność:
$\frac{1}{(c+1)^2}<0,000001$
$(c+1)^2>1000000$
$c+1>\sqrt{1000000}=1000$
$c>999$
Stwierdzamy, że obliczone wartości c są dodatnie, co zgadza się z wcześniejszym założeniem.
Zad. 3. Ze względu na symetrię czworościanu foremnego przyjmujemy, że P(X=1) = P(X=2) = P(X=3) = P(X=4) = P(X=5) = P(X=6) = ¼. Dla wyznaczenia dystrybuanty zmiennej losowej X musimy rozpatrzyć wartości t z pięciu przedziałów:
- jeśli t < 1, to P(X≤t) = 0,
- jeśli t∈[1,2), to P(X≤t) = P(X=1) = ¼,
- jeśli t∈[2,3), to P(X≤t) = P(X=1 lub X=2) = P(X=1)+P(X=2) = ¼+¼ = ½,
- jeśli t∈[3,4), to P(X≤t) = P(X=1 lub X=2 lub X=3) = P(X=1)+P(X=2)+P(X=3) = ¼+¼+¼ = ¾,
- jeśli t≥4, to P(X≤t) = P(X=1 lub X=2 lub X=3 lub X=4) = P(X=1)+P(X=2)+P(X=3)+P(X=4) = ¼+¼+¼+¼ = 1.
W takim razie
$F(x)=\left\{\begin{array}{cl} 0, & t<1 \\ \frac{1}{4}, & t\in [1,2) \\ \frac{1}{2},& t\in[2,3) \\ \frac{3}{4},& t\in[3,4) \\ 1,& t\geq 4 \end{array}\right. .$
Zad. 1. Rozważmy prawdopodobieństwo tego, że zmienna losowa X znajduje się w przedziale pomiędzy naturalną liczbą nieparzystą i następującą po niej liczbą parzystą, czyli P(2k+1<X<2k), gdzie k jest pewną liczbą naturalną. Zgodnie z odpowiednią własnością dystrybuanty mamy:
$P(X\in [2k+1, 2k])=F(2k+2)-F(2k+1)=$
$=\left[1-\left(\frac{1}{2}\right)^{2k+2}\right]-\left[1-\left(\frac{1}{2}\right)^{2k+1}\right]=\left(\frac{1}{2}\right)^{2k+1}-\left(\frac{1}{2}\right)^{2k+2}=$
$=\left(\frac{1}{2}\right)^{2k}\cdot\frac{1}{2}-\left(\frac{1}{2}\right)^{2k}\cdot\left(\frac{1}{2}\right)^2=\left(\frac{1}{2}\right)^{2k}\left[\frac{1}{2}-\left(\frac{1}{2}\right)^2\right]=\left[\left(\frac{1}{2}\right)^2\right]^k \left[\frac{1}{2}-\frac{1}{4}\right]=\left(\frac{1}{4}\right)^k\cdot\frac{1}{4}$
W takim razie
$P(X\in [1,2]\cup[3,4]\cup[5,6]\cup\dots)=$
$=P(X\in [1,2] \ \text{lub} \ X\in [3,4] \ \text{lub} \ X\in [5,6] \ \text{lub} \dots)=$
$=P(X\in [1,2])+P(X\in [3,4])+P(X\in [5,6])+\dots=$
$=P(X\in [2\cdot 0+1,2\cdot 0+2])+P(X\in [2\cdot 1+1,2\cdot 1+2])+\dots=$
$=\frac{1}{4}\cdot \left(\frac{1}{4}\right)^0 + \frac{1}{4}\cdot \left(\frac{1}{4}\right)^1 + \frac{1}{4}\cdot \left(\frac{1}{4}\right)^2 + \dots=\frac{1}{4}\left[1+\frac{1}{4}+\left(\frac{1}{4}\right)^2+\dots\right]=\frac{1}{4}\cdot \frac{1}{1-\frac{1}{4}}=$
$=\frac{1}{4}\cdot \frac{4}{3}=\frac{1}{3}.$
Uwaga. W treści zadania obecne były błędy edytorskie (już zostały usunięte). W związku z tym wszyscy uczestnicy, którzy przysłali rozwiązania zadań w listopadowym etapie ligi, otrzymują punkt za to zadanie bez względu na to, czy i jak je rozwiązali. Autor serdecznie przeprasza za zaistniałą sytuację.
Zad. 2. Załóżmy, że podana funkcja jest gęstością pewnej zmiennej losowej X. Wówczas zgodnie z definicją gęstości wyrażnie P(0≤X≤4) byłoby równe polu pod wykresem gęstości nad przedziałem [0,4], a zatem byłoby równe polu trójkąta prostokątnego o długościach pprzyprostokątnych równych 2 i 4 czyli wynosiłoby ½·2·4=4. Tymczasem prawdopodobieństwo zawsze jest liczbą z przedziału [0,1].
Zwracam uwagę, że dystrybuanta może być funkcją nieciągłą (patrz: przykład 2). Należy jedynie zauważyć, że jeśli dystrybuanta jest funkcją nieciągłą, to nie istnieje gęstość tejże zmiennej losowej.
Zad. 3. Ze względu na to, że 4 daje resztę z dzielenia przez 4 równą 0, 1 i 5 dają resztę z dzielenia przez 4 równą 1, 2 i 3 dają resztę z dzielenia przez 2 równą 0 zaś 3 daje resztę z dzielenia przez 4 równą 3, przyjmujemy, że P(X=0) = 1/6, P(X=1) = P(X=2) = 2/6 i P(X=3) = 1/6. Dla wyznaczenia dystrybuanty zmiennej losowej X musimy rozpatrzyć podzielić zbiór liczb rzeczywistych na pięć przedziałów:
- jeśli t < 0, to P(X≤t) = 0,
- jeśli t∈[0,1), to P(X≤t) = P(X=0) = 1/6,
- jeśli t∈[1,2), to P(X≤t) = P(X=0 lub X=1) = P(X=0)+P(X=1) = 1/6+2/6 = 3/6 = 1/2,
- jeśli t∈[2,3), to P(X≤t) = P(X=0 lub X=1 lub X=2) = P(X=0)+P(X=1)+P(X=2) = 1/6+2/6+2/6 = 5/6 ,
- jeśli t∈[3,4), to P(X≤t) = P(X=0 lub X=1 lub X=2 lub X=3) = P(X=0)+P(X=1)+P(X=2)+P(X=3) = 1/6+2/6+2/6+1/6 = 1.
W takim razie
$F(x)=\left\{\begin{array}{cl} 0, & t<0 \\ \frac{1}{6}, & t\in [0,1) \\ \frac{1}{2},& t\in[1,2) \\ \frac{5}{6},& t\in[2,3) \\ 1,& t\geq 3 \end{array}\right. .$







