 Sformułowania:
Sformułowania:
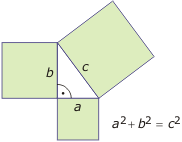
- W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
- Jeżeli trójkąt jest prostokątny, to suma pól kwadratów zbudowanych na przyprostokątnych jest równa polu kwadratu zbudowanego na przeciwprostokątnej.
Twierdzenie odwrotne:
- Jeżeli w trójkącie suma kwadratów długości dwóch boków jest równa kwadratowi długości trzeciego boku, to kąt leżący naprzeciw tego boku jest prosty.
- Jeżeli w trójkącie suma pól kwadratów zbudowanych na dwóch krótszych bokach jest równa polu kwadratu zbudowanego na najdłuższym boku, to trójkąt jest prostokątny, jeśli suma ta jest mniejsza, to trójkąt jest rozwartokątny, a jeśli większa - to ostrokątny.
Dowody:
- Dwa animowane dowody twierdzenia Pitagorasa można znaleźć na Portalu tutaj.
- Ciekawy "chodnikowy" dowód twierdzenia Pitagorasa znajdziesz też na Portalu w tekście Matematyka pod stopami (2) w dziale MATEMATYKA WOKÓL NAS > Na co dzień.
- Dowód z podobieństwa trójkątów:
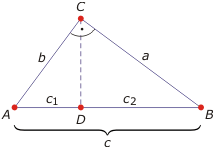
Δ ADC ≈ Δ CDB ≈ Δ ABC (cecha KKK)
Z podobieństw tych zachodzą proporcje:
a:c = c2:a, czyli a2 = c2c
b:c = c1:b, czyli b2 = c1c.
Stąd a2 + b2 = c(c1+c2) = c2 ckd.
- Dowód twierdzenia odwrotnego przeprowadza się bardzo prosto z wykorzystaniem twierdzenia prostego. Niech dany będzie trójkąt o bokach długości a, b, c spełniających a2+ b2 = c2. Weźmy boki a, b i ustawmy je pod kątem prostym. Z prostego twierdzenia Pitagorasa wynika, że trzeci bok tak otrzymanego trójkąta będzie miał długość c. Jednak z cechy BBB przystawania trójkątów ten nowy trójkąt jest przystający do wyjściowego, zatem wyjściowy był trójkątem prostokątnym.
Zastosowania:
Twierdzenie proste stosujemy do:
- obliczenia długości trzeciego boku trójkąta prostokątnego, gdy znane są długości dwóch pozostałych boków,
- wyznaczenia odległości punktów na płaszczyźnie lub w przestrzeni z układem współrzędnych,
Twierdzenie odwrotne stosujemy, aby
- zbudować model kąta prostego,
- sprawdzić, czy trójkąt o danych bokach jest prostokątny, ostrokątny czy rozwartokątny,
Uogólnienia:
- Wersja przestrzenna - w czworościanie prostokątnym (tzn. takim, gdzie 3 krawędzie wychodzące z pewnego wierzchołka są parami prostopadłe) suma kwadratów pól trzech ścian przyprostokątnych (tzn. leżących przy kącie prostym czworościanu) jest równa kwadratowi pola ściany przeciwprostokątnej.
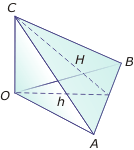
PΔAOB2 + PΔAOC2 + PΔBOC2 = (1/2·AB·h)2 + (1/2·OA·OC)2 + (1/2·OB·OC)2 =
= (1/2·AB·h)2 + 1/4·OC2(OA2 + OB2) = 1/4·AB2·h2 + 1/4·OC2·AB2 =
= 1/4·AB2(h2 + OC2) = 1/4·AB2·H2 = (1/2·AB·H)2 = PΔABC2 ckd.
- Wersja n-wymiarowa - analogię tego twierdzenia można sformułować w wyższych wymiarach.
- Twierdzenie figuralne - jeżeli trójkąt jest prostokątny, to suma pól dowolnych figur podobnych zbudowanych na przyprostokątnych jest równa polu figury podobnej do poprzednich zbudowanej na przeciwprostokątnej (dowód jest łatwy, wystarczy rozważyć skale podobieństwa figur i skorzystać ze zwykłego twierdzenia Pitagorasa).
- Twierdzenie kosinusów - jest to uogólnienie twierdzenia Pitagorasa na trójkąty nieprostokątne, samo twierdzenie Pitagorasa jest szczególnym przypadkiem twierdzenia kosinusów.
- Twierdzenie odwrotne do twierdzenia Pitagorasa znane było na długo przed Pitagorasem. W starożytnym Egipcie i Babilonie stosowano je ok. 4 tys. lat p.n.e. bez dowodu jako regułę wyznaczania kąta prostego.
- Twierdzenie Pitagorasa zostało udowodnione w Szkole Pitagorejskiej w VI w. p.n.e. Nie wiadomo, czy przez samego Pitagorasa, bo dla podniesienia rangi odkrycia uczniowie często nazywali twierdzenia nazwiskiem mistrza.
- Podczas prac nad dowodem twierdzenia Pitagorasa odkryto istnienie odcinków niewspółmiernych, czyli takich, których nie da się zmierzyć, używając tej samej jednostki (tzn. nie da się jej odłożyć całkowitą liczbę razy w każdym z nich). Dziś wiemy, że stosunek długości takich odcinków jest liczbą niewymierną. Z tym odkryciem wiąże się rozpad Szkoły Pitagorejskiej.
- Na przełomie XVIII i XIX w. matematyk niemiecki Karol Gauss odkrył, że jest to twierdzenie geometrii euklidesowej i nie zachodzi w geometriach nieeuklidesowych.







