Karty matematyczne

Jest to zestaw 110 kart wyglądem przypominających tradycyjne karty do gry. Jednak w miejscu liczb i figur karty czerwone zawierają wyniki tabliczki mnożenia w zakresie do 100, a katy czarne - iloczyny odpowiadające tym wynikom. Karty pomyślane są jako pomoc dla klas I-III SP do nauki tabliczki mnożenia na pamięć. Pomóc maja w tym liczne gry, których opisy znajdują się w książkach Andrzeja Grabowskiego pt. "Gry, zabawy i ćwiczenia z tabliczką mnożenia" (część I i II). Rezultaty osiągnięte w niektórych grach zależą tylko od stopnia znajomości tabliczki mnożenia, inne zawierają elementy szybkościowe i manualne, a jeszcze inne - losowe, więc nawet słabsi uczniowie mają czasem szansę wygrać z najlepszymi rachmistrzami w klasie. 

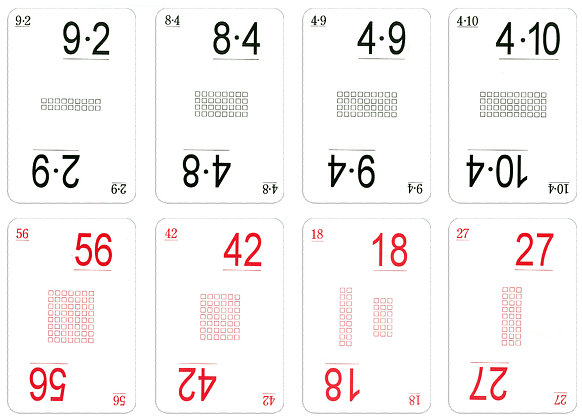
Założony cel karty realizują w sensowny sposób. Niestety, ani autor pomocy, ani rzeczoznawcy ministerialni nie wzięli pod uwagę faktu, że pamięciowe opanowanie tabliczki mnożenia z punku widzenia dydaktyki matematyki nie jest celem istotnym, a od "wykucia" jej na blachę znacznie ważniejsza jest umiejętność tworzenia strategii rachunkowych (jak widać przekonanie, że w matematyce liczy się "pamięciówka" a nie myślenie, jest dość powszechne wśród nauczycieli innych przedmiotów). 

Trzeba mieć świadomość, że pamięciowe podejście do tabliczki mnożenia przynieść może więcej szkody niż pożytku. Uczeń znający standardowa tabliczkę mnożenie na pamięć jest bowiem bezradny w sytuacji, kiedy ma pomnożyć np. 17 razy 5. Nie zna tego wyniku i nie wie, jak sobie z tym poradzić. Uczeń wytrenowany w tzw. "sprytnych rachunkach" od razu wie, że to 170:2, czyli 50+35.

Szkoda, że takiego właśnie podejścia do uczenia tabliczki mnożenia nie zastosowali twórcy kart matematycznych. Wtedy ich zestaw wyglądałby trochę inaczej, inna zapewne byłyby też część proponowanych gier. Podniósłby się wtedy wiek odbiorców pomocy, którą można by śmiało wykorzystywać do ćwiczenia rachunków także w klasach IV-VI szkoły podstawowej, a nawet w gimnazjum. W obecnej sytuacji nauczycielom matematyki nie pozostaje nic innego jak opracować własny zestaw kart, wykonać je własnym sumptem, drukując na twardszym papierze i dopiero tak przygotowane używać do zaproponowanych w książce gier.

Niestety, tylko nieliczne z oryginalnie opracowanych gier dają się w sensowny sposób wykorzystać, gdy zależy nam na ćwiczeniu u dzieci myślenia i technik sprytnych rachunków, a nie podejścia pamięciowego na kartach oryginalnych. Poniżej podajemy przykłady. Można je przeprowadzać bez żadnych zmian lub z niewielkimi tylko modyfikacjami na zestawie oryginalnych kart, a znajomość tabliczki mnożenia na pamięć nie jest w nich wcale potrzebna, a często nawet bardziej przeszkadza niż pomaga w szybkim podaniu wyniku. Rozważmy bowiem następujące zadania:

• Ile wynosi 7·4 + 4·3?
  zamiast mnożenia pamięciowego i dodawania 28+12 wystarczy skorzystać z rozdzielności mnożenia względem dodawania i mamy 4·10
• Czy 7·4 + 4·3 dzieli się przez 3?
  zamiast obliczania wyniku i badania jego podzielności zauważamy, że drugi jest podzielny przez 3, a pierwszy nie, wobec czego suma nie może dzielić się przez 3.

Trzy życia
W grze może brać udział od 2 do 10 zawodników. Prowadzący tasuje karty z iloczynami liczb od 1 do 10 (czarne) i ogłasza wariant gry: liliput, olbrzym lub loteria. W lilipucie celem jest uzyskanie jak najmniejszego wyniku, w olbrzymie – jak największego, a w loterii wyniku jak najbardziej zbliżonego do liczby podanej przez prowadzącego. Prowadzący rozdaje graczom po 3 karty z działaniami. Każdy z zawodników może wymienić od 0 do 2 kart na nowe. Następnie odkłada zakrytą jedną kartę, a pozostałe dwie kładzie odkryte przed sobą i oblicza sumę iloczynów z kart. Zawodnicy kolejno podają otrzymane wyniki. Za podanie błędnej odpowiedzi zawodnik jest wycofywany z następnego rozdania, a w ostatnim rozdaniu traci wszystkie zdobyte punkty. Zawodnicy, którzy uzyskali najlepsze w danym rozdaniu wyniki, zdobywają punkty (np. 3, 2, 1). Po każdym rozdaniu karty są tasowane przez prowadzącego, przekładane przez jednego z zawodników i rozpoczyna się kolejne rozdanie. Grę można powtarzać wielokrotnie, zmieniając warianty i wartości liczb w loterii. Po zakończeniu rozgrywki gracze dodają zdobyte punkty i na tej podstawie wyłaniany jest zwycięzca. Gra zawiera element losowości, dzięki czemu nie tylko najlepsi klasowi rachmistrzowie mają szanse na wygraną.

Prymus
Na każdym stanowisku leżą zakryte jednakowe zestawy kart z działaniami (np. 3 stosy po 3 karty). Zawodnik oblicza sumę iloczynów w stosie, zapisuje na kartce i zakrywa karty z tego stosu. To samo robi kolejno z pozostałymi stosami. Na koniec oblicza pisemnie łączną sumę zapisanych wyników. Po zakończeniu zadania podnosi rękę, co powoduje zatrzymanie czasu. Za każdy błąd i za każdą dodatkowo zapisaną liczbę dolicza się 30 sekund karnych.

Szeryf
W grze bierze udział 4 graczy. Wszyscy opierają ręce na stole. Prowadzący wykłada kolejno na stół karty z wynikami lub działaniami i jednocześnie podaje pewną liczbę. Jeśli liczba z karty jest podzielna przez wymienioną, gracze przykrywają kartę ręką. Osoba, której ręka jest na spodzie, otrzymuje 1 pkt. Jeśli gracz oderwie rękę od stołu w wypadku, gdy wyłożona liczba nie ma żądanej podzielności, otrzymuje (-1) pkt. Rozgrywkę można powtarzać wielokrotnie, sumując uzyskane punkty. 

Do niektórych gier wykorzystuje się pudełka z przegródkami, które można zakupić razem z kartami lub wykonać samodzielnie ze sklejki. Do takich gier należy np.

Olimpijczyk
Na każdym stanowisku do gry znajdują się dwa pudełka z przegródkami oraz stos potasowanych kart z działaniami i wynikami. Na dany sygnał zawodnicy dobierają karty w pary „działanie-wynik” i układają do przegródek. Po zakończeniu zadania podnoszą rękę, co powoduje zatrzymanie czasu. Za każdy błąd dolicza się 30 sekund karnych.  

Opisywane tutaj karty i gry są wykorzystywane m.in. w corocznych Mistrzostwach Wrocławia w Szybkim Liczeniu oraz były wykorzystywane w Mistrzostwach Polski w Tabliczce Mnożenia, które odbywały się do 2009 roku.